
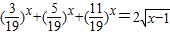 实根的个数是( )
实根的个数是( ) +
+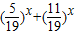 -
-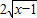 ,其定义域为x∈[1,+∞),先判断其单调性,再判断其是否存在零点即可.
,其定义域为x∈[1,+∞),先判断其单调性,再判断其是否存在零点即可.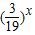 +
+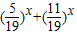 -
-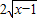 ,其定义域为x∈[1,+∞).
,其定义域为x∈[1,+∞).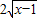 在定义域上单调递增,∴-
在定义域上单调递增,∴-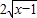 在定义域上单调递减;而
在定义域上单调递减;而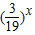 、
、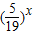 、
、 在定义域x∈[1,+∞)上单调递减,
在定义域x∈[1,+∞)上单调递减,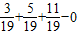 =1>0,f(2)=
=1>0,f(2)=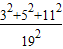 -2<1-2=-1<0,即f(1)×f(2)<0,
-2<1-2=-1<0,即f(1)×f(2)<0,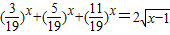 实根的个数是1.
实根的个数是1.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com