分析:方法一(1)取BC
1的中点为R,连接RE,RF,通过证明四边形AFRE为平行四边形 得出AF∥RE,再证出直线AF∥平面BEC
1;
(2)延长C
1E交CA延长线于点Q,连接QB,则∠C
1BC为平面BEC
1和平面ABC所成的锐二面角的平面角.在△BCC
1中求解即可.
方法二:
(1)以点F为坐标原点,FA为x轴,FB为y轴,FS为z轴建立空间直角坐标系,设平面BEC
1的法向量为
,可以利用
⊥来证明.
(2)利用BEC
1的一个法向量与平面ABC一个法向量夹角求出二面角A-EC-F的大小.
解答:解:法一(1)取BC
1的中点为R,连接RE,RF,
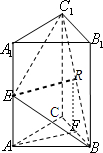
则RF∥CC
1,AE∥CC
1,且AE=RF,…(3分)
则四边形AFRE为平行四边形,
则AF∥RE,AF?平面REC
1.RE?平面REC
1.∴AF∥平面REC
1.…(6分)
(2)延长C
1E交CA延长线于点Q,连接QB,
则QB即为平面BEC
1与平面ABC的交线,
由于EA∥C1C,E为AA
1的中点,∴A为QC中点,∴QA=AC=AB,
∴∠ABCQ=∠AQB=
∠CAB=30°,
∴∠CBQ=∠CBA+∠ABQ=60°+30°=90°,
∴BC⊥BQ,又QB⊥B1B,∴QB⊥面C
1CBB
1,
∴C
1B⊥BQ,
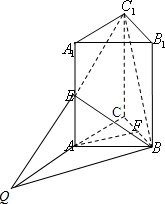
则∠C
1BC为平面BEC
1和平面ABC所成的锐二面角的平面角.…(8分)
在△BCC
1中,
cos∠C1BC=== =平面BEC
1和平面ABC所成的锐二面角的余弦值为
.
…(12分)
法二 取B
1C
1中点为S,连接FS,
以点F为坐标原点,FA为x轴,FB为y轴,FS为z轴建立空间直角坐标系,
则
A(,0,0),B(0,1,0),F(0,0,0),C(0,-1,0),
A1(,0,4),B1(0,1,4),C(0,-1,4),E(,0,2),…(2分)
(1)则
=(-,0,0),
=(,-1,2),=(0,-2,4),
设平面BEC
1的法向量为
=(x1,y1,z1),
则
•=0,•=0,即
…(4分)
令y
1=2,则x
1=0,z
1=1,即
=(0,2,1),所以
•=0,
故直线AF∥平面BEC
1.…(6分)
(2)设平面ABC的法向量
=(0,0,1),
则
cosθ==.
由于平面BEC
1和平面ABC所成二面角是锐二面角
所以其余弦值是
.
…(12分)
点评:本题考查空间直线、平面位置关系的判断,二面角大小求解,考查空间想象能力、推理论证、计算、转化能力.利用向量这一工具,解决空间几何体问题,能够降低思维难度.

 (2011•黑龙江一模)已知三棱柱ABC-A1B1C1,底面三角形ABC为正三角形,侧棱AA1⊥底面ABC,AB=2,AA1=4,E为AA1的中点,F为BC中点.
(2011•黑龙江一模)已知三棱柱ABC-A1B1C1,底面三角形ABC为正三角形,侧棱AA1⊥底面ABC,AB=2,AA1=4,E为AA1的中点,F为BC中点.



 阅读快车系列答案
阅读快车系列答案 (2011•黑龙江一模)已知三棱柱ABC-A1B1C1,底面三角形ABC为正三角形,侧棱AA1⊥底面ABC,AB=2,AA1=4,E为AA1的中点,F为BC中点.
(2011•黑龙江一模)已知三棱柱ABC-A1B1C1,底面三角形ABC为正三角形,侧棱AA1⊥底面ABC,AB=2,AA1=4,E为AA1的中点,F为BC中点.