
分析 (1)可设f(x)=ax2+bx+c,从而由f(0)=1可得c=1,而根据f(x+1)-f(x)=2x可以得到2ax+a+b=2x,从而可以求出a,b,从而得出f(x)=x2-x+1;
(2)由f(x)>2x+m恒成立得到x2-3x+1>m恒成立,可令h(x)=x2-3x+1,可判断h(x)在[-1,1]上单调递减,从而得到h(x)的最小值,这样即可求出m的范围;
(3)先求出g(t)=4t2-(4a+2)t+a2+a+1,该函数的对称轴为t=$\frac{1+2a}{4}$,可讨论对称轴和0的关系:分$\frac{1+2a}{4}≥0$,和$\frac{1+2a}{4}<0$两种情况,然后可求出每种情况的g(t)的最大值.
解答 解:(1)设f(x)=ax2+bx+c(a≠0),因为f(0)=1,所以c=1;
∵f(x+1)-f(x)=2x;
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x;
∴2ax+a+b=2x;
∴$\left\{\begin{array}{l}2a=2\\ a+b=0\end{array}\right.$;
解得:$\left\{\begin{array}{l}a=1\\ b=-1\end{array}\right.$;
∴f(x)=x2-x+1;
(2)当x∈[-1,1]时,f(x)>2x+m恒成立即:x2-3x+1>m恒成立;
令$h(x)={x^2}-3x+1={(x-\frac{3}{2})^2}-\frac{5}{4}$,x∈[-1,1];
因为对称轴$x=\frac{3}{2}$>1,所以g(x)在上[-1,1]上递减;
∴h(x)min=h(1)=-1;
∴m<-1;
∴实数m的范围为(-∞,-1);
(3)g(t)=f(2t-a)=4t2-(4a+2)t+a2+a+1,t∈[-1,1],对称轴为:$t=\frac{1+2a}{4}$;
①当$\frac{1+2a}{4}≥0$,即:$a≥-\frac{1}{2}$时,$g{(t)_{max}}=g(-1)=4+(4a+2)+{a^2}+a+1={a^2}+5a+7$;
②当$\frac{1+2a}{4}<0$,即:$a<-\frac{1}{2}$时,$g{(t)_{max}}=g(1)=4-(4a+2)+{a^2}+a+1={a^2}-3a+3$;
综上所述:$g(t)_{max}=\left\{\begin{array}{l}{{a}^{2}+5a+7}&{a≥-\frac{1}{2}}\\{{a}^{2}-3a+3}&{a<-\frac{1}{2}}\end{array}\right.$.
点评 考查二次函数的一般形式,根据f(x)求f[g(x)]的方法,多项式相等时,对应项的系数相等,根据二次函数的单调性求最值,要熟悉二次函数的图象.


科目:高中数学 来源: 题型:选择题
| A. | 周期为2π的偶函数 | B. | 周期为2π的奇函数 | ||
| C. | 周期为π的偶函数 | D. | 周期为π的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
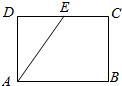
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($1,\frac{5}{4}$] | B. | ($\frac{5}{4},\frac{3}{2}$] | C. | $(\frac{5}{4},\frac{13}{8})$ | D. | ($\frac{5}{4},\frac{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | x=-$\frac{π}{2}$是函数f(x)的一条对称轴 | |
| B. | φ的所有取值中,绝对值最小的是$\frac{5π}{4}$ | |
| C. | ($\frac{π}{2}$,0)是函数f(x)的一个对称中心 | |
| D. | 若f(x1)-f(x2)=4,则|x1-x2|的最小值为$\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com