试题分析:(1)由2+4=6,2+6=8,2+8=10,4+6=10,4+8=12,6+8=14,
得l(P)=5
由2+4=6,2+8=10,2+16=18,4+8=12,4+16=20,8+16=24,
得l(Q)=6
(2)不妨设a
1<a
2<a
3<…<a
n,可得
a
1+a
2<a
1+a
3<…<a
1+a
n<a
2+a
n<a
3+a
n<…<a
n-1+a
n,
故a
i+a
j (1≤i<j≤n)中至少有2n-3个不同的数,即l(A)≥2n-3.
事实上,设a
1,a
2,a
3,…,a
n成等差数列,考虑a
i+a
j (1≤i<j≤n),根据等差数列的性质,当i+j≤n时, a
i+a
j=a
1+a
i+j-1;当i+j>n时, a
i+a
j=a
i+j-n+a
n;
因此每个和a
i+a
j(1≤i<j≤n)等于a
1+a
k(2≤k≤n)中的一个,或者等于a
l+a
n(2≤l≤n-1)中的一个.故对这样的集合A,l(A)=2n-3,所以l(A)的最小值为2n-3.
点评:新定义问题,利用新定义集合确定
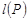
,
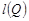
属于简单问题。而求
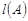
的最小值的方法,则具有一定难度,特别是假设“排序”难以想到,这是解决问题的关键所在。

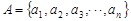 ,其中
,其中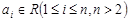 ,
,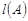 表示
表示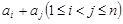 的所有不同值的个数.
的所有不同值的个数.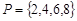 ,
,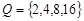 ,分别求
,分别求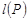 ,
,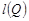 ;
;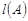 的最小值.
的最小值.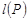 ,
,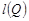 属于简单问题。而求
属于简单问题。而求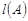 的最小值的方法,则具有一定难度,特别是假设“排序”难以想到,这是解决问题的关键所在。
的最小值的方法,则具有一定难度,特别是假设“排序”难以想到,这是解决问题的关键所在。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案