
(2006
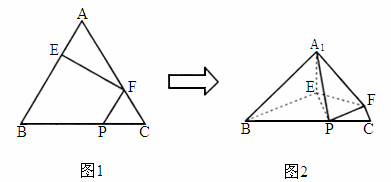
江苏,19)如下图,在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE∶EB=CF∶FA=CP∶PB=l∶2(如图1).将△AEF沿EF折起到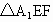 的位置,使二面角
的位置,使二面角 成直二面角,连结
成直二面角,连结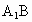 、
、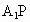 (如图2).
(如图2).
(1)
求证: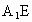 ⊥平面BEP;
⊥平面BEP;
(2)
求直线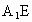 与平面
与平面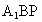 所成角的大小;
所成角的大小;
(3)
求二面角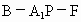 的大小(用反三角函数值表示).
的大小(用反三角函数值表示). |
解析:不妨设正三角形 ABC的边长为3.(1) 在图1中,取BE的中点D,连结DF.∵ AE∶EB=CF∶FA=1∶2,∴AF=AD=2,而∠ A=60°,∴△ ADF是正三角形.又AE=DE=1,∴ EF⊥AD.在图2中,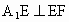 , ,
BE ⊥EF,∴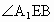 为二面角 为二面角 的平面角. 的平面角.
由题设条件知此二面角为直二面角, ∴ 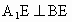 . .
又 BE∩EF=E,∴ ⊥平面BEF, ⊥平面BEF,
即  ⊥平面BEP. ⊥平面BEP.
(2) 在图2中,∵ 不垂直于 不垂直于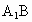 , ,
∴  是平面 是平面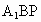 的斜线. 的斜线.
又  ⊥平面BEP,∴ ⊥平面BEP,∴ ⊥BP, ⊥BP,
从而 BP垂直于 在平面 在平面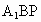 内的射影(三垂线定理的逆定理). 内的射影(三垂线定理的逆定理).
设  在平面 在平面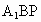 内的射影为 内的射影为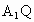 ,且 ,且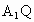 交BP于点Q,则 交BP于点Q,则 就是 就是 与平面 与平面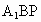 所成的角. 所成的角.
且 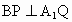 .在△EBP中, .在△EBP中,
∵ BE=BP=2,∠EBP=60°,∴△ EPB是等边三角形,∴BE=EP.又 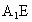 ⊥平面BEP,∴ ⊥平面BEP,∴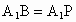 , ,
∴ Q为BP的中点,且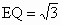 , ,
又 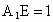 ,在Rt△ ,在Rt△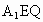 中, 中,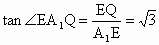 ,∴ ,∴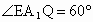 .所以直线 .所以直线 与平面 与平面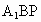 所成的角为60°. 所成的角为60°.
(3) 在图3中,过F作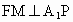 于M,连结QM、QF. 于M,连结QM、QF.
∵ CF=CP=1,∠C=60°,∴△ FCP是正三角形,∴PF=1.又 ∵  ⊥平面BEP, ⊥平面BEP, , ,
∴ 从而 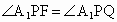 , ② , ②
由①②及 MP为公共边知△FMP≌△QMP,∴∠ QMP=∠FMP=90°,且MF=MQ,从而∠ FMQ为二面角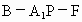 的平面角.在Rt 的平面角.在Rt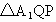 中, 中,
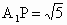 . .
∵ 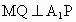 ,∴ ,∴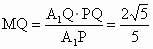 , ,
∴ 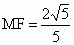 . .
在△ FCQ中,FC=1,QC=2,∠C=60°,由余弦定理得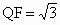 . .
在△ FMQ中,cos∠FMQ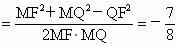 . .
所以二面角  . . |


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com