
已知函数 ,
,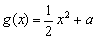 (
( 为常数),函数
为常数),函数 图象上横坐标为
图象上横坐标为 的点处的切线
的点处的切线 ,与函数
,与函数 的图象相切.
的图象相切.
(Ⅰ)求直线 的方程及
的方程及 的值;
的值;
(Ⅱ)若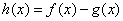 ,求函数
,求函数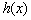 的极值.
的极值.
解:(Ⅰ)由题意得: 与函数y=
与函数y=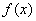 图象的切点为(1,
图象的切点为(1,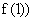
∵切点(1,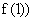 在
在 图象上
图象上
∴切点为(1,0) ………………………………………………………………………2分
又∵

∴直线 的斜率为:
的斜率为: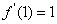 …………………………………………………………4分
…………………………………………………………4分
∴直线 的
的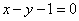 ……………………………………………………………………5分
……………………………………………………………………5分
∵直线 与函数y=
与函数y= 的图象相切
的图象相切
∴方程组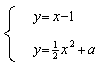
 只有一个解,即方程
只有一个解,即方程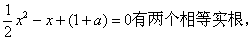
∴△=0,解得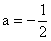 ……………7分
……………7分
(Ⅱ)由(I)得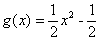
∴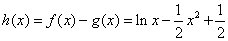 ,且
,且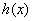 的定义域为
的定义域为 ……………9分
……………9分
又∵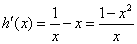
令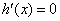 ,得
,得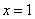 ,或
,或 (舍去)…………………11分
(舍去)…………………11分
当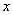 变化时,
变化时,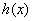 ,
,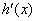 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
| 单调递增 |
| 单调递减 |
…………………13分
∴当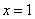 时,函数
时,函数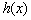 有极大值,极大值为
有极大值,极大值为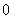 ,函数
,函数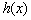 没有极小值。………14分
没有极小值。………14分


科目:高中数学 来源: 题型:
在极坐标系中,圆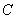 的方程为
的方程为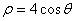 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为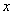 轴的正半轴建
轴的正半轴建
立平面直角坐标系,直线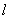 的参数方程为
的参数方程为 (
(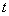 为参数).
为参数).
(1)写出圆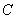 的直角坐标方程以及直线
的直角坐标方程以及直线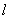 的普通方程;
的普通方程;
(2)求直线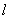 被圆
被圆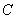 所截得的弦长.
所截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知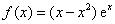 ,给出以下几个结论:①
,给出以下几个结论:①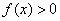 的解集是{x|0<x<1};②
的解集是{x|0<x<1};②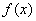 既有极小值,又有极大值;③
既有极小值,又有极大值;③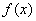 没有最小值,也没有最大值;④
没有最小值,也没有最大值;④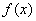 有最大值,没有最小值.其中判断正确的是_______.
有最大值,没有最小值.其中判断正确的是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列函数中,既是偶函数又在区间(﹣∞,0)上单调递增的是()
A. f(x)=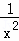 B. f(x)=x2+1 C. f(x)=x3 D. f(x)=2﹣x
B. f(x)=x2+1 C. f(x)=x3 D. f(x)=2﹣x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com