
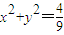 ,直线l:y=kx+m与椭圆C:
,直线l:y=kx+m与椭圆C: 相交于P、Q两点,O为原点.
相交于P、Q两点,O为原点.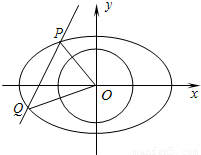
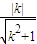 =
=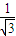 即可求得k,从而可得直线l的方程;
即可求得k,从而可得直线l的方程;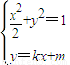 得:(1+2k2)x2+4kmx+2m2-2=0,利用韦达定理可求得x1+x2=-
得:(1+2k2)x2+4kmx+2m2-2=0,利用韦达定理可求得x1+x2=-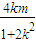 ,又△POQ重心恰好在圆x2+y2=
,又△POQ重心恰好在圆x2+y2= 上,可求得
上,可求得 +
+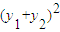 =4,化简可求得m2=
=4,化简可求得m2=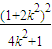 ,△>0⇒1+2k2>m2,二者联立即可求得m的范围.
,△>0⇒1+2k2>m2,二者联立即可求得m的范围.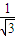 ,
,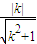 ,
, =
=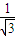 ,解得k=±
,解得k=±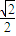 .
.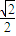 (x+1).
(x+1).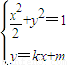 得:(1+2k2)x2+4kmx+2m2-2=0.
得:(1+2k2)x2+4kmx+2m2-2=0.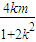 .
. 上,
上,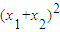 +
+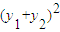 =4,
=4,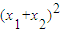 +
+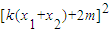 =4,即(1+k2)
=4,即(1+k2)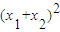 +4km(x1+x2)+4m2=4.
+4km(x1+x2)+4m2=4.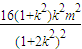 -
-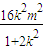 +4m2=4,化简得:m2=
+4m2=4,化简得:m2=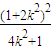 ,代入(⊕)式得:k≠0,
,代入(⊕)式得:k≠0,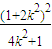 =1+
=1+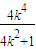 =1+
=1+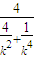 .
.

科目:高中数学 来源: 题型:
 已知圆O:x2+y2=r2(r>0)与直线x-y+2
已知圆O:x2+y2=r2(r>0)与直线x-y+2| 2 |
| ||
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:河北省宣化一中2012届高三新课标高考模拟数学文科试题 题型:044
选修4-4:坐标系与参数方程
在极坐标系下,已知圆O:![]() 和直线
和直线![]() ,
,
(1)求圆O和直线l的直角坐标方程;
(2)当![]() 时,求直线l与圆O公共点的一个极坐标.
时,求直线l与圆O公共点的一个极坐标.
查看答案和解析>>
科目:高中数学 来源:黑龙江省哈尔滨市第六中学2011届高三第一次模拟考试数学试题(文史类) 题型:047
已知直线![]() 所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到F的最小距离为2
所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到F的最小距离为2
(1)求椭圆C的标准方程;
(2)已知圆O:![]() ,直线l:
,直线l:![]() ,当点
,当点![]() 在椭圆C上运动时,直线l与圆O是否相交于两个不同的点A,B?若相交,试求弦长|AB|的取值范围,否则说明理由.
在椭圆C上运动时,直线l与圆O是否相交于两个不同的点A,B?若相交,试求弦长|AB|的取值范围,否则说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省高考模拟冲刺(提优)测试一理科数学试卷(解析版) 题型:解答题
已知圆O: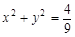 ,直线l:
,直线l: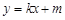 与椭圆C:
与椭圆C: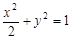 相交于P、Q两点,O为原点.
相交于P、Q两点,O为原点.
(Ⅰ)若直线l过椭圆C的左焦点,且与圆O交于A、B两点,且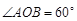 ,求直线l的方程;
,求直线l的方程;
(Ⅱ)如图,若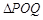 重心恰好在圆上,求m的取值范围.
重心恰好在圆上,求m的取值范围.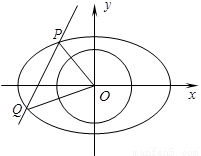
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com