
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数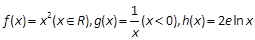 .有下列命题:
.有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4;
③ 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
C
解析试题分析:(1) =
=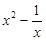 ,
,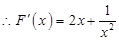 ,则
,则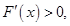 解得
解得 ,所以
,所以 在
在 内单调递增;故①正确.
内单调递增;故①正确.
(2) 和
和 之间存在“隔离直线”,设“隔离直线”为
之间存在“隔离直线”,设“隔离直线”为 ,当“隔离直线”与
,当“隔离直线”与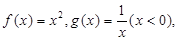 同时相切时,截距最小,令切点坐标为
同时相切时,截距最小,令切点坐标为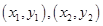 ,则切线方程为
,则切线方程为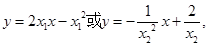 所以
所以 ,故
,故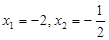 ,所以
,所以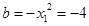 ,此时截距最小,故②正确;此时斜率为
,此时截距最小,故②正确;此时斜率为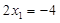 ,k的取值范围是
,k的取值范围是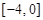 .故③错误.
.故③错误.
④令F(x)=h(x)-m(x)=x2-2elnx(x>0),再令F′(x)═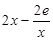 =0,x>0,得x=
=0,x>0,得x= ,
,
从而函数h(x)和m(x)的图象在x= 处有公共点.
处有公共点.
因此存在h(x)和m(x)的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k,则
隔离直线方程为y-e=k(x- ),即y=kx-k
),即y=kx-k +e.
+e.
由h(x)≥kx-k +e可得 x2-kx+k
+e可得 x2-kx+k -e≥0当x∈R恒成立,
-e≥0当x∈R恒成立,
则△=k2-4k +4e=
+4e=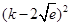 ≤0,只有k=2
≤0,只有k=2 时,等号成立,此时直线方程为:y=2
时,等号成立,此时直线方程为:y=2 x-e.
x-e.
同理证明,由φ(x )≤kx-k +e,可得只有k=2
+e,可得只有k=2 时,等号成立,此时直线方程为:y=2
时,等号成立,此时直线方程为:y=2 x-e.
x-e.
综上可得,函数f(x)和g(x)存在唯一的隔离直线y=2 x-e,故④正确.
x-e,故④正确.
考点:函数恒成立问题;复合命题的真假;利用导数研究函数的极值


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:单选题
设平面 与平面
与平面 相交于直线
相交于直线 ,直线
,直线 在平面
在平面 内,直线
内,直线 在平面
在平面 内,且
内,且 ,则
,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
给出下列四个命题:
①梯形的对角线相等;②对任意实数x,均有 ;
;
③不存在实数x,使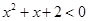 ;④有些三角形不是等边三角形;
;④有些三角形不是等边三角形;
其中真命题的个数为( )
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com