
已知函数 .
.
(I)判断函数 在
在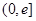 上的单调性(
上的单调性(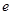 为自然对数的底);
为自然对数的底);
(II)记 为
为 的导函数,若函数
的导函数,若函数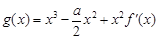 在区间
在区间 上存在极值,求实数
上存在极值,求实数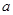 的取值范围。
的取值范围。
(I)若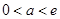 ,当
,当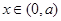 时
时 ,函数
,函数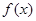 在
在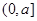 上单调递减,
上单调递减,
当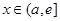 时
时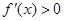 ,函数
,函数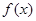 在
在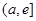 上单调递增,
上单调递增,
若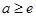 ,则
,则 ,函数
,函数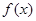 在
在 上单调递减.
上单调递减.
(II)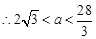 。
。
【解析】本试题主要是考查了导数的在研究函数中的运用。判定函数单调区间,以及函数的极值问题的综合运用
(1)由已知函数得到导函数,然后对于参数a分类讨论得到其单调区间,注意讨论的完备性。
(2)要是函数在给定区间存在极值,说明了导数值为零的点在该点左右两侧函数值异号,那么借助于概念分析求解。
解:(I)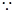
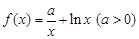
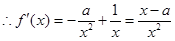 …………1分
…………1分
若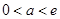 ,当
,当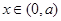 时
时 ,函数
,函数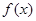 在
在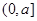 上单调递减,
上单调递减,
当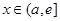 时
时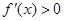 ,函数
,函数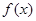 在
在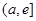 上单调递增,…………5分
上单调递增,…………5分
若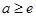 ,则
,则 ,函数
,函数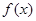 在
在 上单调递减.
…………7分
上单调递减.
…………7分
(II)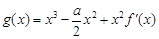
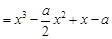 ,
, 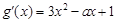 , …………8分
, …………8分
方法一:函数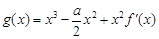 在区间
在区间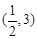 上存在极值
上存在极值
等价为关于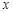 方程
方程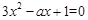 在
在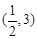 上有变号实根
上有变号实根
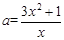 ……11分
……11分 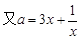 在
在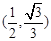 上单调递减,在
上单调递减,在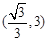 上单调递增。
上单调递增。
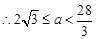 …………14分
…………14分
当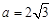 时,
时,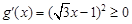 ,不存在极值
,不存在极值
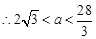 ……15分
……15分
方法二: 等价为关于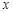 方程
方程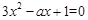 在
在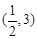 上有变号实根。
上有变号实根。
⑴ 关于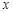 方程
方程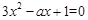 在
在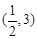 上有两个不相等实数根;
上有两个不相等实数根;
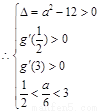
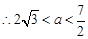 …………10分
…………10分
⑵关于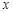 方程
方程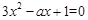 在
在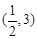 上有一个实数根;
上有一个实数根;
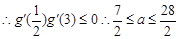 …………12分
…………12分
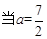 时,
时,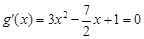 的解为
的解为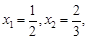
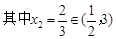 符合题意
符合题意 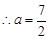 …………13分
…………13分
当 时,
时,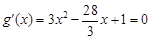 的解为
的解为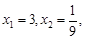
均不符合题意 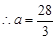 (舍)………14分 综上所述,
(舍)………14分 综上所述,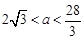 .………15分
.………15分


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年崇文区二模文)(14分)
已知直线![]() ,抛物线
,抛物线![]() ,定点M(1,1)。
,定点M(1,1)。
(I)当直线![]() 经过抛物线焦点F时,求点M关于直线
经过抛物线焦点F时,求点M关于直线![]() 的对称点N的坐标,并判断点N 是否在抛物线C上;
的对称点N的坐标,并判断点N 是否在抛物线C上;
(II)当![]() 变化且直线
变化且直线![]() 与抛物线C有公共点时,设点P(a,1)关于直线
与抛物线C有公共点时,设点P(a,1)关于直线![]() 的对称点为Q(x0,y0),求x0关于k的函数关系式
的对称点为Q(x0,y0),求x0关于k的函数关系式![]() ;当
;当![]() 且P与M重合时,求
且P与M重合时,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年崇文区二模理)(14分)
已知直线![]() ,抛物线
,抛物线![]() ,定点M(1,1)。
,定点M(1,1)。
(I)当直线![]() 经过抛物线焦点F时,求点M关于直线
经过抛物线焦点F时,求点M关于直线![]() 的对称点N的坐标,并判断点N 是否在抛物线C上;
的对称点N的坐标,并判断点N 是否在抛物线C上;
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年崇文区二模理)(14分)
已知直线![]() ,抛物线
,抛物线![]() ,定点M(1,1)。
,定点M(1,1)。
(I)当直线![]() 经过抛物线焦点F时,求点M关于直线
经过抛物线焦点F时,求点M关于直线![]() 的对称点N的坐标,并判断点N 是否在抛物线C上;
的对称点N的坐标,并判断点N 是否在抛物线C上;
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线![]() ,抛物线
,抛物线![]() ,
,
定点M(1,1)。
(I)当直线![]() 经过抛物线焦点F时,求点M关于直线
经过抛物线焦点F时,求点M关于直线![]() 的对称点N的坐标,并判断点N 是否在抛物线C上;
的对称点N的坐标,并判断点N 是否在抛物线C上;
(II)当![]() 变化且直线
变化且直线![]() 与抛物线C有公共点时,设点P(a,1)关于直线
与抛物线C有公共点时,设点P(a,1)关于直线![]() 的对称点为Q(x0,y0),求x0关于k的函数关系式
的对称点为Q(x0,y0),求x0关于k的函数关系式![]() ;若P与M重合时,求
;若P与M重合时,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com