
(本小题8分)设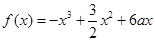 .
.
(1)当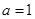 时,求
时,求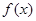 在区间
在区间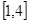 上的最值;
上的最值;
(2)若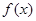 在
在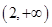 上存在单调递增区间,求
上存在单调递增区间,求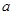 的取值范围.
的取值范围.
科目:高中数学 来源:2014届吉林省高一下学期第三次月考理科数学试卷(解析版) 题型:解答题
(本小题8分)设等差数列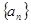 的前
的前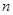 项和为
项和为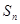 ,已知
,已知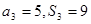 ,
,
(1)求首项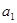 和公差
和公差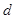 的值;
的值;
(2)若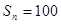 ,求
,求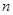 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2010年浙江省高一上学期期中考试数学试卷 题型:解答题
(本小题8分) 设函数 (常数
(常数
(1)求 的定义域;
的定义域;
(2)在函数 的图像上是否存在不同的两点,使得过这两点的直线平行于x轴?
的图像上是否存在不同的两点,使得过这两点的直线平行于x轴?
(3)当 满足什么条件时,
满足什么条件时, 在
在 上恒取正值。
上恒取正值。
查看答案和解析>>
科目:高中数学 来源:2010年浙江省高一上学期期中考试数学试卷 题型:解答题
(本小题8分) 嘉兴市秀洲区为促进淡水鱼养殖业的发展,将价格控制在适当范围内,并决定对淡水鱼养殖提供政府补贴。设淡水鱼的市场价格为 ,政府补贴为
,政府补贴为 。根据市场调查,当
。根据市场调查,当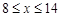 时,淡水鱼的市场日供应量
时,淡水鱼的市场日供应量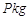 与市场日需求量
与市场日需求量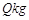 近似满足关系:
近似满足关系: ,
,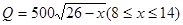 ;当
;当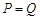 时的市场价格称为市场平衡价格。
时的市场价格称为市场平衡价格。
(1) 将政府补贴费表示为市场平衡价格的函数,并求出函数的定义域;
(2)为使市场平衡价格不高于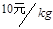 ,政府需要补贴吗?如果需要,至少为多少
,政府需要补贴吗?如果需要,至少为多少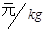 ?
?
查看答案和解析>>
科目:高中数学 来源:2010年广东省高一第二学期期末测试数学试题 题型:解答题
(本小题8分) 已知数列 的前
的前 项和为
项和为 ,点
,点 在直线
在直线 上;数列
上;数列 满足
满足 ,且
,且 ,它的前9项和为153.
,它的前9项和为153.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和为
项和为 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com