
在直三棱柱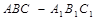 中,
中,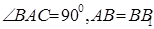 ,直线
,直线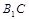 与平面
与平面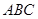 成30°角.
成30°角.
(I)求证:平面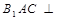 平面
平面 ;
;
(II)求直线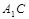 与平面
与平面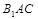 所成角的正弦值;
所成角的正弦值;
(III)求二面角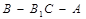 的平面角的余弦值.
的平面角的余弦值.

(1)见解析;(2)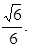 (3)
(3) .
.
【解析】本试题主要考查了空间想象能力的运用,解决空间中的线面角二面角以及面面垂直的判定定理的运用。

(1)证明:由直三棱柱性质,B1B⊥平面ABC,
∴B1B⊥AC,
又BA⊥AC,B1B∩BA=B,
∴AC⊥平面 ABB1A1,
又AC 平面B1AC,
平面B1AC,
∴平面B1AC⊥平面ABB1A1.
(2)解:过A1做A1M⊥B1A1,垂足为M,连结CM,
∵平面B1AC⊥平面ABB1A,且平面B1AC∩平面ABB1A1=B1A,
∴A1M⊥平面B1AC.
∴∠A1CM为直线A1C与平面B1AC所成的角,
∵直线B1C与平面ABC成30°角,
∴∠B1CB=30°.
设AB=BB1=a,可得B1C=2a,BC=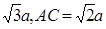 ,
,

∴直线A1C与平面B1AC所成角的正弦值为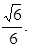
(3)解:过A做AN⊥BC,垂足为N,过N做NO⊥B1C,垂足为O,连结AO,[来源:Zxxk.Com]
由AN⊥BC,可得AN⊥平面BCC1B1,由三垂线定理,可知AO⊥B1C,
∴∠AON为二面角B—B1C—A的平面角,



科目:高中数学 来源:2014届辽宁沈阳高二寒假验收数学试卷(解析版) 题型:解答题
(本小题满分10分)
如图,在直三棱柱 中,
中, ,
, .棱
.棱 上有两个动点E,F,且EF =" a" (a为常数).
上有两个动点E,F,且EF =" a" (a为常数).

(Ⅰ)在平面ABC内确定一条直线,使该直线与直线CE垂直;
(Ⅱ)判断三棱锥B—CEF的体积是否为定值.若是定值,求出这个三棱锥的体积;若不是定值,说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省高三第四次月考理科数学 题型:解答题
(本小题满分12分)
如图,在直三棱柱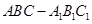 中,
中,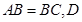 、
、 分别为
分别为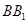 、
、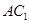 的中点。
的中点。
(I)证明:ED为异面直线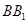 与
与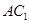 的公垂线;
的公垂线;
(II)设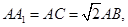 求二面角
求二面角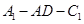 的大小。
的大小。

查看答案和解析>>
科目:高中数学 来源:河北省保定市高二年级第二学期期中联考数学试卷(文科) 题型:解答题
(本题满分12分)在直三棱柱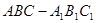 中,
中, ,直线
,直线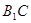 与平面
与平面 成
成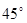 角;
角;
(1)求证:平面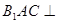 平面
平面 ;
;
(2)求二面角 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源:2010年湖北普通高等学校招生全国统一考试数学(文史类)模拟试题 题型:解答题
(本小题满分12分)如图,在直三棱柱 中,
中,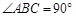 ,
,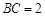 ,
, ,
, ,E在
,E在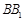 上,且
上,且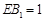 ,
,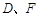 分别为
分别为 的中点.
的中点.
(1)求证: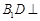 平面
平面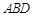 ;
;
(2)求异面直线 与
与 所成的角;
所成的角;
(3)求点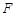 到平面
到平面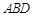 的距离.
的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com