
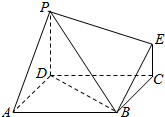
 如图为一简单组合体,其底面ABCD为边长2正方形,PD⊥平面ABCD,EC∥PD,且$PD=2\sqrt{2},CE=\sqrt{2}$.
如图为一简单组合体,其底面ABCD为边长2正方形,PD⊥平面ABCD,EC∥PD,且$PD=2\sqrt{2},CE=\sqrt{2}$. 分析 (1)证法1:连结AC与BD交于点F,连结NF,证明DB⊥AC,AC⊥PD,推出AC⊥面PBD,然后证明NE⊥面PDB.
证法2:如图以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系,求出相关点坐标,推出EN⊥PB,EN⊥DB,然后证明NE⊥面PDB.
(2)连结DN,证明DN⊥PB,求出平面PBE的法向量,求出平面ABCD的法向量,设平面PBE与平面ABCD所成的二面角为θ,利用数量积求解平面PBE与平面ABCD所成的二面角.
解答 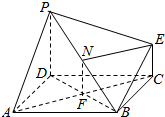 (本题12分)
(本题12分)
解:(1)证法1:连结AC与BD交于点F,连结NF,
∵F为BD的中点,∴NF∥PD且$NF=\frac{1}{2}PD$
又EC∥PD且$EC=\frac{1}{2}PD$,则NF∥EC且NF=EC
∴四边形NFCE为平行四边形∴NE∥FC------(2分)
∵DB⊥AC,PD⊥平面ABCD,AC?平面ABCD∴AC⊥PD,
又PD∩BD=D,∴AC⊥面PBD------(4分)
∴NE⊥面PDB------(5分)
证法2:如图以点D为坐标原点,以AD所在的直线为x轴建立空间直角坐标系如图示:则$B(2,2,0),C(0,2,0),P(0,0,2\sqrt{2}),E(0,2,\sqrt{2}),N(1,1,\sqrt{2})$
则$\overrightarrow{EN}=(1,-1,0),\overrightarrow{PB}=(2,2,-2\sqrt{2}),\overrightarrow{DB}=(2,2,0)$------(2分)
∵$\overrightarrow{EN}•\overrightarrow{PB}=1×2-1×2+0×(-2\sqrt{2})=0$,$\overrightarrow{EN}•\overrightarrow{DB}=1×2-1×2+0×0=0$
∴EN⊥PB,EN⊥DB------(4分)
∵PB,DB?面PDB,且PB∩DB=B
∴NE⊥面PDB------(5分)
(2)连结DN,由(1)知NE⊥面PDB∴DN⊥NE,
∵$PD=DB=2\sqrt{2}$,∴DN⊥PB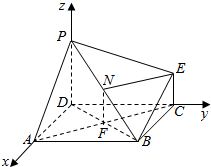
∴$\overrightarrow{DN}$为平面PBE的法向量,且$\overrightarrow{DN}=(1,1,\sqrt{2})$------(8分)
∵$\overrightarrow{DP}$为平面ABCD的法向量,$\overrightarrow{DP}=(0,0,2\sqrt{2})$,------(9分)
设平面PBE与平面ABCD所成的二面角为θ,则$cosθ=\frac{{\overrightarrow{DN}•\overrightarrow{DP}}}{{|{\overrightarrow{DN}}||{\overrightarrow{DP}}|}}=\frac{{\sqrt{2}}}{2}$------(11分)
∴θ=45°,即平面PBE与平面ABCD所成的二面角为45°------(12分)
点评 本题考查直线与平面垂直的判定定理的应用,二面角的平面角的求法,考查计算能力以及逻辑推理能力.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 焦点在x轴的椭圆 | B. | 焦点在y轴的椭圆 | ||
| C. | 圆或焦点在x轴的椭圆 | D. | 圆或焦点在y轴的椭圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 5 | C. | 3 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\sqrt{3}$x | C. | y=±$\frac{\sqrt{3}}{2}$x | D. | y=±$\frac{2\sqrt{3}}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com