
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|x>1} | C. | R | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某高校青年志愿者协会,组织大一学生开展一次爱心包裹劝募活动,将派出的志愿者,分成甲、乙两个小组,分别在两个不同的场地进行劝募,每个小组各6人,爱心人士每捐购一个爱心包裹,志愿者就将送出一个钥匙扣作为纪念,茎叶图记录了这两个小组成员某天劝募包裹时送出钥匙扣的个数,且图中乙组的一个数据模糊不清,用x表示,已知甲组送出钥匙扣的平均数比乙组的平均数少一个.
某高校青年志愿者协会,组织大一学生开展一次爱心包裹劝募活动,将派出的志愿者,分成甲、乙两个小组,分别在两个不同的场地进行劝募,每个小组各6人,爱心人士每捐购一个爱心包裹,志愿者就将送出一个钥匙扣作为纪念,茎叶图记录了这两个小组成员某天劝募包裹时送出钥匙扣的个数,且图中乙组的一个数据模糊不清,用x表示,已知甲组送出钥匙扣的平均数比乙组的平均数少一个.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
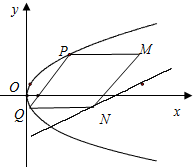 抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,反之亦然.如图所示,今有抛物线y2=2px(p>0),一光源在点M($\frac{41}{4}$,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线l:2x-4y-17=0上的点N,再反射后又射回点M,设P,Q两点的坐标分别是(x1,y1),(x2,y2),
抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,反之亦然.如图所示,今有抛物线y2=2px(p>0),一光源在点M($\frac{41}{4}$,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线l:2x-4y-17=0上的点N,再反射后又射回点M,设P,Q两点的坐标分别是(x1,y1),(x2,y2),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com