
| A. | $\frac{2016}{2017}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2014}{2015}$ | D. | 1 |
分析 求出$\overrightarrow{O{A}_{n}}$•$\overrightarrow{a}$,|$\overrightarrow{O{A}_{n}}$|,|$\overrightarrow{a}$|,代入夹角公式求出cosθn,得出sinθn,找到$\frac{cos{θ}_{n}}{sin{θ}_{n}}$的表达式,代入计算即可.
解答 解:An=(n,$\frac{1}{n+1}$),$\overrightarrow{O{A}_{n}}$=(n,$\frac{1}{n+1}$),∴|$\overrightarrow{O{A}_{n}}$|=$\sqrt{{n}^{2}+(\frac{1}{n+1})^{2}}$=$\frac{\sqrt{{n}^{2}({n+1)}^{2}+1}}{n+1}$,|$\overrightarrow{a}$|=1,$\overrightarrow{O{A}_{n}}$•$\overrightarrow{a}$=$\frac{1}{n+1}$,
∴cosθn=$\frac{\overrightarrow{O{A}_{n}}•\overrightarrow{a}}{|\overrightarrow{O{A}_{n}}|•|\overrightarrow{a}|}$=$\frac{1}{\sqrt{{n}^{2}(n+1)^{2}+1}}$,∴sinθn=$\frac{n(n+1)}{\sqrt{{n}^{2}(n+1)^{2}+1}}$,∴$\frac{cos{θ}_{n}}{sin{θ}_{n}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$,
∴$\frac{{cos{θ_1}}}{{sin{θ_1}}}+\frac{{cos{θ_2}}}{{sin{θ_2}}}+…+\frac{{cos{θ_{2016}}}}{{sin{θ_{2016}}}}$=1-$\frac{1}{2}$+$\frac{1}{2}-\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{2016}-\frac{1}{2017}$=1-$\frac{1}{2017}$=$\frac{2016}{2017}$.
故选A.
点评 本题考查了向量数量积的运算,向量的夹角公式,数列求和,属于中档题.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 23 | B. | 95 | C. | 135 | D. | 138 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {y|y≥0} | B. | {y|y>0} | C. | {y|y≥1} | D. | {y|y>1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
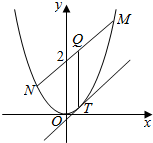 已知抛物线C:x${\;}^{2}=\frac{1}{2}y$,直线y=kx+2交C于M、N两点,Q是线段MN的中点,过Q作x轴的垂线交C于点T.
已知抛物线C:x${\;}^{2}=\frac{1}{2}y$,直线y=kx+2交C于M、N两点,Q是线段MN的中点,过Q作x轴的垂线交C于点T.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com