
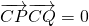 ( C为圆心).则该圆的半径为________,m的值为________.
( C为圆心).则该圆的半径为________,m的值为________.

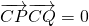 得到CP⊥CQ,即三角形CPQ为等腰直角三角形,根据余弦函数定义得到d=CPcos45°,求出CP的长,即为圆C的半径,然后用求出的圆的半径等于表示出的半径r,列出关于m的方程,求出方程的解得到m的值.
得到CP⊥CQ,即三角形CPQ为等腰直角三角形,根据余弦函数定义得到d=CPcos45°,求出CP的长,即为圆C的半径,然后用求出的圆的半径等于表示出的半径r,列出关于m的方程,求出方程的解得到m的值. )2+(y-3)2=
)2+(y-3)2=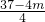 ,
,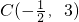 ,半径
,半径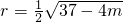 ,
,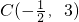 圆心到直线x+2y-3=0的距离d=
圆心到直线x+2y-3=0的距离d=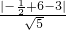 =
= .
.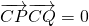 ,
, d=
d= ,即圆C的半径为
,即圆C的半径为 ,
,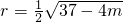 =
= ,解得:
,解得: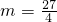 .
. ;
;


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com