
| A. | 2015 | B. | 2016 | C. | 4030 | D. | 4031 |
分析 等差数列{an}中,a1>0,a2015+a2016>0,a2015a2016<0,可得等差数列{an}是单调递减数列,d<0,因此a2015>0,a2016<0,利用求和公式可得:S4030>0,S4031<0,即可得出结论.
解答 解:∵等差数列{an}中,a1>0,a2015+a2016>0,a2015a2016<0,
∴等差数列{an}是单调递减数列,d<0,因此a2015>0,a2016<0,
∴S4030=$\frac{4030({a}_{1}+{a}_{4030})}{2}$=$\frac{4030({a}_{2015}+{a}_{2016})}{2}$>0,
S4031=$\frac{4031({a}_{1}+{a}_{4031})}{2}$=4031a2016<0,
∴使前n项和Sn>0成立的最大自然数n是4030.
故选:C.
点评 本题考查了等差数列的通项公式与求和公式及其性质、数列的单调性,考查了推理能力与计算能力,属于中档题.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 0或1 | B. | 1或2 | C. | 0或2 | D. | 1或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
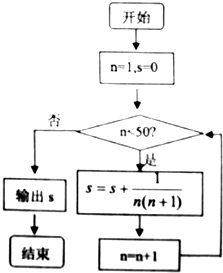 某算法的程序框图如图所示,则执行该算法后输出的结果为( )
某算法的程序框图如图所示,则执行该算法后输出的结果为( )| A. | $\frac{39}{40}$ | B. | $\frac{49}{50}$ | C. | $\frac{50}{49}$ | D. | $\frac{60}{59}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤2} | B. | {x|-1≤x≤0} | C. | {x|1≤x≤2} | D. | {x|0≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<b<a | C. | a<c<b | D. | c<a<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com