
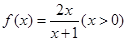
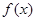 在
在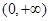 上为单调增函数;
上为单调增函数;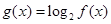 ,求
,求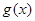 的值域;
的值域; 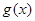 ,若关于
,若关于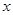 的方程
的方程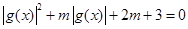 有三个不同的实数解,求
有三个不同的实数解,求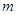 的取值范围.
的取值范围.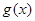 值域为
值域为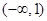 ;(3)
;(3)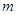 的取值范围为
的取值范围为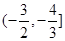 。
。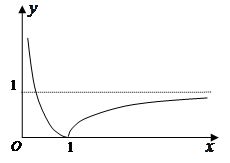
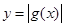 可知其图像,然后徐结合图像,
可知其图像,然后徐结合图像,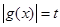 ,则
,则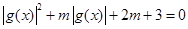 有三个不同的实数解,即为
有三个不同的实数解,即为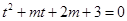 有两个根,且一个在
有两个根,且一个在 上,一个在
上,一个在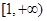 上,然后分析得到m的范围。
上,然后分析得到m的范围。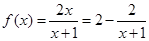 ,设
,设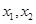 是
是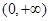 上的任意两个数,且
上的任意两个数,且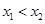 ,……2分
,……2分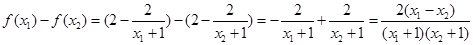 ……4分
……4分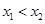 ,∴
,∴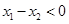 ,∴
,∴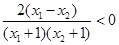 即
即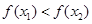
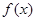 在
在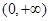 上为增函数, …………………………6分
上为增函数, …………………………6分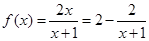 ,
,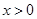 ,所以
,所以 ,所以
,所以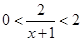 ,
,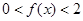 …………………………8分
…………………………8分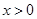 时,
时,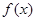 单调递增,
单调递增,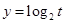 单调递增,
单调递增,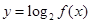 单调递增,所以
单调递增,所以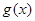 值域为
值域为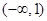 …………………………10分
…………………………10分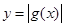 大致图象如右图所示,
大致图象如右图所示,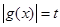 ,则
,则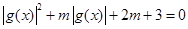 有三个不同的实数解,即为
有三个不同的实数解,即为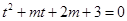 有两个根,且一个在
有两个根,且一个在 上,一个在
上,一个在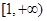 上,设
上,设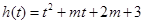 ………12分
………12分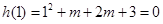 ,
,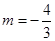 ,此时另一根为
,此时另一根为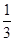 适合题意; ………………13分
适合题意; ………………13分 ,得
,得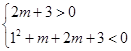 ,∴
,∴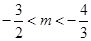
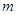 的取值范围为
的取值范围为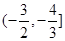 …………………………16分
…………………………16分

科目:高中数学 来源:不详 题型:填空题
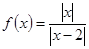 为偶函数; (2)函数
为偶函数; (2)函数 ;
;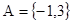 ,
,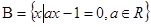 ,若
,若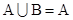 ,则实数
,则实数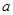 的取值集合为
的取值集合为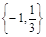 ; (4)集合
; (4)集合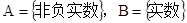 ,对应法则f:“求平方根”,则
,对应法则f:“求平方根”,则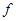 是A到B的映射;你认为正确命题的序号是 (把正确的序号都写上).
是A到B的映射;你认为正确命题的序号是 (把正确的序号都写上).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com