
郑(本题满分14分)已知定点A(0,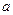 )(
)(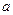 >0),直线
>0),直线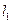 :
: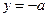 交
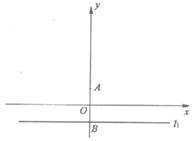
交 轴于点B,记过点A且与直线l1相切的圆的圆心为点C.
轴于点B,记过点A且与直线l1相切的圆的圆心为点C.
(I)求动点C的轨迹E的方程;
(Ⅱ)设倾斜角为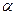 的直线
的直线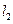 过点A,交轨迹E于两点 P、Q,交直线
过点A,交轨迹E于两点 P、Q,交直线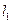 于点R.
于点R.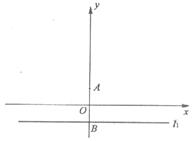
(1)若tan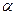 =1,且ΔPQB的面积为
=1,且ΔPQB的面积为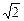 ,求
,求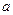 的值;
的值;
(2)若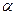 ∈[
∈[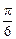 ,
,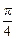 ],求|PR|·|QR|的最小值.
],求|PR|·|QR|的最小值.
解法一:(Ⅰ)连CA,过C作CD⊥l1,垂足为D,由已知可得|CA|=|CD|,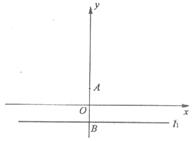
∴点C的轨迹是以A为焦点,l1为准线的抛物线,
∴轨迹E的方程为x2=4ay …………………(4分)
(Ⅱ)直线l2的方程为y=kx+a,与抛物线方程联立消去y得
x2-4akx-4a2=0.
记P(x1,y1),Q(x2,y2),
则x1+x2=4ak,x1x2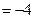 a2<0. …………(6分)
a2<0. …………(6分)
(1)若tanα=1,即k=1,此时x1+x2=4a, x1x2=-4a2.
∴SΔBPQ=SΔABP+SΔABQ=a|x1|+a|x2|=a|x2-x1|
=a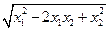 =a
=a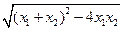 =a
=a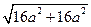 =4
=4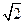 a2 . …………(8分)
a2 . …………(8分)
∴4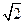 a2=
a2=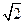 ,注意到a>0,∴a =
,注意到a>0,∴a =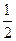 ………………………………(9分)
………………………………(9分)
(2) 因为直线PA的斜率k≠O,易得点R的坐标为(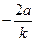 ,-a). ……(10分)
,-a). ……(10分)
|PR|·|QR|=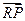 ·
·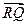 =(x1+
=(x1+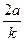 ,y1+a)·(x2+
,y1+a)·(x2+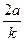 ,y2+a)
,y2+a)
=(x1+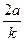 )(x2+
)(x2+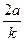 )+(kx1+2 a)(kx2+ 2a)
)+(kx1+2 a)(kx2+ 2a)
=(1+k2) x1 x2+(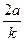 +2 ak)( x1+x2)+
+2 ak)( x1+x2)+ 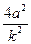 +4a2
+4a2
= -4a2(1+k2)+4ak(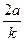 +2ak)+
+2ak)+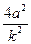 +4a2 =4a2(k2+
+4a2 =4a2(k2+ )+8a2≥8a2+8a2=16a2
)+8a2≥8a2+8a2=16a2
又α∈[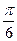 ,
,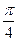 ],∴k∈[
],∴k∈[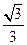 ,1],
,1],
当且仅当k2= , 即k=1时取到等号. ……………………(12分)
, 即k=1时取到等号. ……………………(12分)
从而|PR|·|QR|的最小值为16a2. ……………………(14分)
解析


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
郑(本题满分14分)已知定点A(0,![]() )(
)( ![]() >0),直线
>0),直线![]() :
:![]() 交
交![]() 轴于点B,记过点A且与直线l1相切的圆的圆心为点C.
轴于点B,记过点A且与直线l1相切的圆的圆心为点C.
(I)求动点C的轨迹E的方程;
(Ⅱ)设倾斜角为![]() 的直线
的直线![]() 过点A,交轨迹E于两点 P、Q,交直线
过点A,交轨迹E于两点 P、Q,交直线![]() 于点R.
于点R.
 (1)若tan
(1)若tan![]() =1,且ΔPQB的面积为
=1,且ΔPQB的面积为![]() ,求
,求![]() 的值;
的值;
(2)若![]() ∈[
∈[![]() ,
,![]() ],求|PR|·|QR|的最小值.
],求|PR|·|QR|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com