Question

正三棱锥V—ABC的底面边长为2，侧棱长为3，过底面AB边的截面交侧棱VC于P.

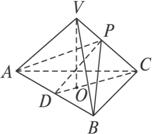
（1）若P为VC的中点，求截面PAB的面积；

（2）求截面PAB的面积的最大值.

Answer 1

解析:（1）∵四面体V—ABC为正三棱锥，

∴V在平面ABC上的射影O为△ABC的中心.连结CO并延长交AB于D，连结DP，则有CD⊥AB.由VO⊥面ABC.

∴AB⊥面VOC.∴AB⊥DP.

在Rt△VOC中，可求OC=.

∴cos∠PCO=OC∶VC=.

由P为VC的中点，根据余弦定理得

PD²=PC²+CD²-2PC·CD·cos∠PCO

=·cos∠PCO=.

∴S_△PAB=·AB·PD=.

（2）由（1）知，VC上任一点P与AB的中点D的连线都是△APB的高，设PC=x(0＜x＜3).

∴PD²=PC²+CD²-2PC·CD·cos∠PCD=x²+3-2·x··=x²-x+3.

∴S_△APB=AB·PD

=×2×≤.

∴（S_△APB）_max=.

小结：对正棱锥的问题，应充分利用正棱锥的性质.求截面ABP面积的最小值，也可直接求D到VC的距离，作△ABP的高DP，此时△ABP的面积最小.