(I)解:f(x)的定义域为(0,+∞),
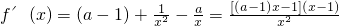
(x>0)
令g(x)=(x-1)[(a-1)x-1],…(1分)
①当a=2时,对任意x∈(0,+∞),f′(x)=
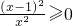
,故f(x)在(0,+∞)上单调递增;
②当a≤1时,
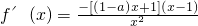
,
∵-[(1-a)x+1]<0对任意x∈(0,+∞)恒成立,
∴x≥1时,f′(x)≤0,0<x<1时,f′(x)>0,
∴函数在[1,+∞)上是增函数,在(0,1)上是减函数;
③当1<a<2时,令f′(x)≤0可得
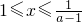
,令f′(x)≥0可得0<x≤1或x≥

,
∴函数在(0,1]和[

,+∞)上是增函数,在[1,

)上是减函数;
(II)证明:(1)当n=1时,左边-右边=
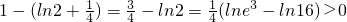
不等式成立…(7分)
(2)假设n=k(k∈N
*)不等式成立,即

…
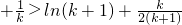
成立
那么,当n=k+1时,左边=
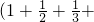
…
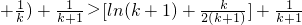
+

…(8分)
下面证明:

即证
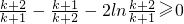
…(9分)
由(Ⅰ)知当a=2时,

在(0,+∞)上单调递增
则对任意k∈N
*,都有
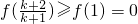
成立
即对任意k∈N
*,都有
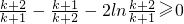
成立
因此n=k+1时成立
由(1)(2)及数学归纳法原理知
原不等式对任意n∈N
*都成立.…(12分)
分析:(I)f(x)的定义域为(0,+∞),求导函数
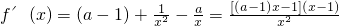
(x>0),令g(x)=(x-1)[(a-1)x-1],分类讨论,确定g(x)的正负,即可得到导函数的正负,从而可得函数的单调性;
(II)利用数学归纳法证明,当n=k+1时,利用分析法进行证明.
点评:本题考查导数知识的运用,考查函数的单调性,考查分类讨论的数学思想,考查不等式的证明,考查数学归纳法与分析法的运用,综合性强.

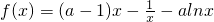 (a≤2)
(a≤2) …
… 对任意n∈N*都成立.
对任意n∈N*都成立.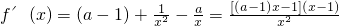 (x>0)
(x>0)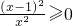 ,故f(x)在(0,+∞)上单调递增;
,故f(x)在(0,+∞)上单调递增;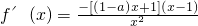 ,
,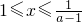 ,令f′(x)≥0可得0<x≤1或x≥
,令f′(x)≥0可得0<x≤1或x≥ ,
, ,+∞)上是增函数,在[1,
,+∞)上是增函数,在[1, )上是减函数;
)上是减函数;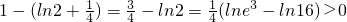
 …
…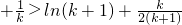 成立
成立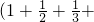 …
…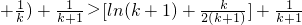 +
+ …(8分)
…(8分)
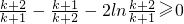 …(9分)
…(9分) 在(0,+∞)上单调递增
在(0,+∞)上单调递增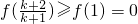 成立
成立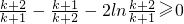 成立
成立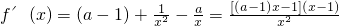 (x>0),令g(x)=(x-1)[(a-1)x-1],分类讨论,确定g(x)的正负,即可得到导函数的正负,从而可得函数的单调性;
(x>0),令g(x)=(x-1)[(a-1)x-1],分类讨论,确定g(x)的正负,即可得到导函数的正负,从而可得函数的单调性;
