
已知各项均为非负整数的数列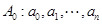
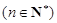 ,满足
,满足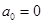 ,
,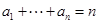 .若存在最小的正整数
.若存在最小的正整数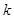 ,使得
,使得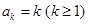 ,则可定义变换
,则可定义变换 ,变换
,变换 将数列
将数列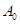 变为数列
变为数列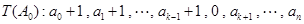 .设
.设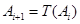 ,
,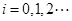 .
.
(Ⅰ)若数列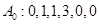 ,试写出数列
,试写出数列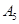 ;若数列
;若数列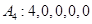 ,试写出数列
,试写出数列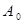 ;
;
(Ⅱ)证明存在唯一的数列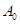 ,经过有限次
,经过有限次 变换,可将数列
变换,可将数列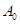 变为数列
变为数列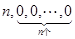 ;
;
(Ⅲ)若数列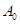 ,经过有限次
,经过有限次 变换,可变为数列
变换,可变为数列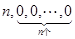 .设
.设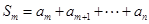 ,
,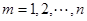 ,求证
,求证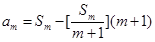 ,其中
,其中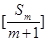 表示不超过
表示不超过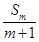 的最大整数.
的最大整数.
解:(Ⅰ)若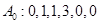 ,则
,则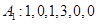 ;
;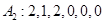 ;
; 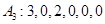 ;
;
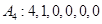 ;
; 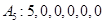 .
.
若 ,则
,则 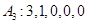 ;
;  ;
;  ;
; 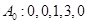 .
………4分
.
………4分
(Ⅱ)先证存在性,若数列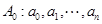 满足
满足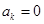 及
及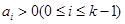 ,则定义变换
,则定义变换 ,变换
,变换 将数列
将数列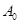 变为数列
变为数列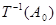 :
: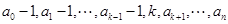 .
.
易知 和
和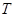 是互逆变换.
………5分
是互逆变换.
………5分
对于数列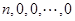 连续实施变换
连续实施变换 (一直不能再作
(一直不能再作 变换为止)得
变换为止)得
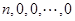
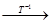
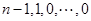
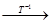
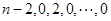
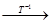
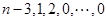
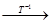
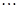
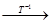
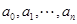 ,
,
则必有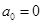 (若
(若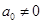 ,则还可作变换
,则还可作变换 ).反过来对
).反过来对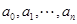 作有限次变换
作有限次变换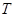 ,即可还原为数列
,即可还原为数列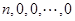 ,因此存在数列
,因此存在数列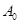 满足条件.
满足条件.
下用数学归纳法证唯一性:当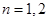 是显然的,假设唯一性对
是显然的,假设唯一性对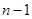 成立,考虑
成立,考虑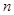 的情形.
的情形.
假设存在两个数列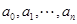 及
及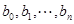 均可经过有限次
均可经过有限次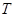 变换,变为
变换,变为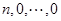 ,这里
,这里 ,
,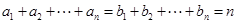
若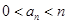 ,则由变换
,则由变换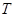 的定义,不能变为
的定义,不能变为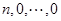 ;
;
若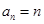 ,则
,则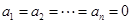 ,经过一次
,经过一次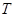 变换,有
变换,有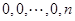
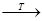

由于 ,可知
,可知 (至少3个1)不可能变为
(至少3个1)不可能变为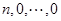 .
.
所以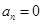 ,同理
,同理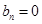 令
令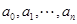
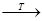
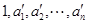 ,
,
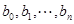
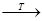
 ,
,
则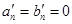 ,所以
,所以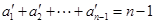 ,
,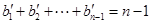 .
.
因为
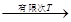
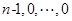 ,
,

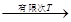
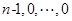 ,
,
故由归纳假设,有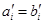 ,
,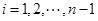 .
.
再由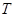 与
与 互逆,有
互逆,有
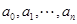
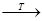
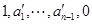 ,
,
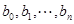
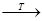
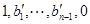 ,
,
所以 ,
,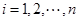 ,从而唯一性得证.
………9分
,从而唯一性得证.
………9分
(Ⅲ)显然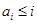
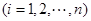 ,这是由于若对某个
,这是由于若对某个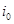 ,
,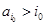 ,则由变换的定义可知,
,则由变换的定义可知,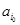 通过变换,不能变为
通过变换,不能变为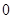 .由变换
.由变换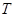 的定义可知数列
的定义可知数列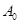 每经过一次变换,
每经过一次变换,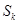 的值或者不变,或者减少
的值或者不变,或者减少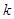 ,由于数列
,由于数列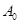 经有限次变换
经有限次变换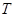 ,变为数列
,变为数列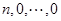 时,有
时,有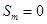 ,
,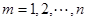 ,
,
所以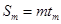
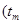 为整数
为整数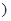 ,于是
,于是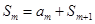
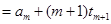 ,
,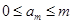 ,
,
所以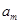 为
为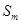 除以
除以 后所得的余数,即
后所得的余数,即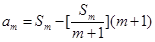 .………13分
.………13分
【解析】略


科目:高中数学 来源: 题型:
| ||
| n个 |
| ||
| n个 |
| Sm |
| m+1 |
| Sm |
| m+1 |
| Sm |
| m+1 |
查看答案和解析>>
科目:高中数学 来源:北京市朝阳区2012届高三3月第一次综合练习数学理科试题 题型:044
已知各项均为非负整数的数列A0∶a0,a1,…,an(n∈N*),满足a0=0,a1+…+an=n.若存在最小的正整数k,使得ak=k(k≥1),则可定义变换T,变换T将数列A0变为数列T(A0)∶a0+1,a1+1,…,ak-1+1,0,ak+1,…,an.设Ai+1=T(Ai),i=0,1,2….
(Ⅰ)若数列A0∶0,1,1,3,0,0,试写出数列A5;若数列A4∶4,0,0,0,0,试写出数列A0;
(Ⅱ)证明存在唯一的数列A0,经过有限次T变换,可将数列A0变为数列![]() ;
;
(Ⅲ)若数列A0,经过有限次T变换,可变为数列![]() .设Sm=am+am+1+…+an,m=1,2,…,n,求证am=Sm-[
.设Sm=am+am+1+…+an,m=1,2,…,n,求证am=Sm-[![]() ](m+1),其中[
](m+1),其中[![]() ]表示不超过
]表示不超过![]() 的最大整数.
的最大整数.
查看答案和解析>>
科目:高中数学 来源:2012年北京市朝阳区高考数学一模试卷(理科)(解析版) 题型:解答题
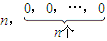 ;
;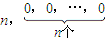 .设Sm=am+am+1+…+an,m=1,2,…,n,求证
.设Sm=am+am+1+…+an,m=1,2,…,n,求证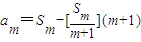 ,其中
,其中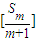 表示不超过
表示不超过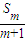 的最大整数.
的最大整数.查看答案和解析>>
科目:高中数学 来源:2012年北京市朝阳区高考数学一模试卷(文科)(解析版) 题型:解答题
 ;
; .设Sm=am+am+1+…+an,m=1,2,…,n,求证
.设Sm=am+am+1+…+an,m=1,2,…,n,求证 ,其中
,其中 表示不超过
表示不超过 的最大整数.
的最大整数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com