练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    满足：（1^）第1行的数高^考#资*源#网为1；（2^）第n（n≥2)行首尾两数高^考#资*源#网均为n，其余的数高^考#资*源#网都等于它肩上的两个数高^考#资*源#网相加．则第n行(n≥2)中第2个数高^考#资*源#网是________________（用n表示^）.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图所示的三角形数阵中，满足：（1）第1行的数为1，（2）第n（n≥2）行首尾两数均为n，其余的数都等于它肩上的两个数相加，则第n+1行中第2个数是
     
    （用n表示）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图的倒三角形数阵满足：（1）第1行的，n个数，分别  是1，3，5，…，2n-1；（2）从第二行起，各行中的每一个数都等于它肩上的两数之和；（3）数阵共有n行．问：当n=2012时，第32行的第17个数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图的三角形数阵中，满足：（1）第1行的数为1；（2）第n（n≥2）行首尾两数均为n，其余的数都等于它肩上的两个数相加．则第n行（n≥2）中第2个数是
    n2-n+2
    2
    n2-n+2
    2
    （用n表示）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图数表满足：（1）第n（n＞1）行首尾两数均为n，第一行为一个数1；（2）表中的递推关系：从第三行起的非首尾两数中的每一个数等于其上一行中它的“肩膀上”的两个数的和．现记第n（n＞1）行第2个数为an，如a2=2，a3=4，a4=7，a5=11…，则可以得到递推关系：an=
    an-1+（n-1）
    an-1+（n-1）
    ，由此通过有关求解可以求得：
    a2011-22009
    =
    1006
    1006
    （用数字填写）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

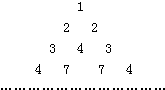    精英家教网一个类似于杨辉三角的三角形数组（如图）满足：（1）第1行只有1个数1；（2）当n≥2时，第n行首尾两数均为n；（3）当n＞2时，中间各数都等于它肩上两数之和，则第n行（n≥2）第2个数是
     
    ．

    查看答案和解析>>

    同步练习册答案