
(12分)已知 数列{an}、{bn}满足,![]() ,且
,且![]() (
(![]() ,
,![]() ),其中
),其中![]() 为数列{an}的前n项和.又
为数列{an}的前n项和.又![]() , 对任意
, 对任意![]() 都成立,
都成立,
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)求数列![]() 的前n项和
的前n项和![]() .
.
科目:高中数学 来源: 题型:
(本小题满分12分)
已知数列![]() ,设
,设![]() ,数列
,数列![]() 。 (1)求证:
。 (1)求证:![]() 是等差数列; (2)求数列
是等差数列; (2)求数列![]() 的前n项和Sn;
的前n项和Sn;
(3)若![]() 一切正整数n恒成立,求实数m的取值范围。
一切正整数n恒成立,求实数m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)已知数列![]() ,其中
,其中![]() 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;![]() 是公差为
是公差为![]() 的等差数列;
的等差数列;![]() 是公差为
是公差为![]() 的等差数列(
的等差数列(![]() ).
).
(1)若![]() ,求
,求![]() ; (2)试写出
; (2)试写出![]() 关于
关于![]() 的关系式,并求
的关系式,并求![]() 的取值范围;(3)续写已知数列,使得
的取值范围;(3)续写已知数列,使得![]() 是公差为
是公差为![]() 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试理科数学卷(辽宁) 题型:解答题
(本小题满分12分)已知数列 ,
, 与函数
与函数 ,
, ,
, 满足条件:
满足条件: ,
, .
.
(I)若 ,
,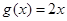 ,
, ,
, 存在,求
存在,求 的取值范围;
的取值范围;
(II)若函数 为
为 上的增函数,
上的增函数, ,
, ,
, ,证明对任意
,证明对任意 ,
, (用
(用 表示).
表示).
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省武汉市武昌区高三五月调研理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知数列 ,
,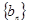 满足:
满足: ,当
,当 时,
时, ;对于任意的正整数
;对于任意的正整数 ,
,
 .设数列
.设数列 的前
的前 项和为
项和为 .
.
(Ⅰ)计算 、
、 ,并求数列
,并求数列 的通项公式;
的通项公式;
(Ⅱ)求满足 的正整数
的正整数 的集合.
的集合.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河北省高三第一次月考理科数学卷 题型:解答题
(本小题满分12分)
已知数列 ,且
,且 是函数
是函数 ,(
,( )的一个极值点.数列
)的一个极值点.数列 中
中 (
( 且
且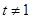 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)记 ,当
,当 时,数列
时,数列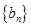 的前
的前 项和为
项和为 ,求使
,求使 的
的 的最小值;
的最小值;
(3)若 ,证明:
,证明: (
( )。
)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com