Question

【题目】已知双曲线 =1（a＞0，b＞0）的右焦点为F（c，0）．
（1）若双曲线的一条渐近线方程为y=x且c=2，求双曲线的方程；
（2）以原点O为圆心，c为半径作圆，该圆与双曲线在第一象限的交点为A，过A作圆的切线，斜率为﹣ ，求双曲线的离心率．

Answer 1

【答案】
（1）解：∵双曲线 的渐近线方程为y=

∴若双曲线的一条渐近线方程为y=x，可得 =1，解之得a=b

∵c= =2，∴a=b=

由此可得双曲线方程为

（2）解：设A的坐标为（m，n），可得直线AO的斜率满足k= = ，即m= n…①

∵以点O为圆心，c为半径的圆方程为x2+y2=c2

∴将①代入圆方程，得3n2+n2=c2，解得n= c，m= c

将点A（ c， c）代入双曲线方程，得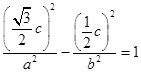

化简得： c2b2﹣ c2a2=a2b2，

∵c2=a2+b2

∴b2=c2﹣a2代入上式，化简整理得 c4﹣2c2a2+a4=0

两边都除以a4，整理得3e4﹣8e2+4=0，解之得e2= 或e2=2

∵双曲线的离心率e＞1，∴该双曲线的离心率e= （舍负）

【解析】（1）根据双曲线的一条渐近线方程为y=x，可得 =1，解得a=b，结合c= =2算出a=b= ，可得该双曲线方程；（2）设A（m，n），根据切线垂直于过切点的半径算出m= n．而以点O为圆心，c为半径的圆方程为x2+y2=c2 ， 将A的坐标代入圆方程，算出点A（ c， c），将此代入双曲线方程，并结合c2=a2+b2化简整理得 c4﹣2c2a2+a4=0，再根据离心率公式整理得3e4﹣8e2+4=0，解之即可得到该双曲线的离心率．