
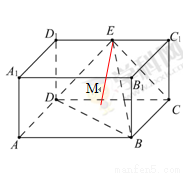
如图,在长方体ABCD—A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.

(1)求证:ED⊥平面EBC;
(2)求三棱锥E-DBC的体积.
(1)见解析;(2)
【解析】
试题分析:
(1)易得△DD1E为等腰直角三角形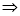 DE⊥EC,BC⊥平面
DE⊥EC,BC⊥平面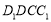
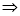 BC⊥DE,所以DE⊥平面EBC
BC⊥DE,所以DE⊥平面EBC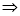 平面DEB⊥平面EBC.
平面DEB⊥平面EBC.
(2)需要做辅助线,取CD中点M,连接EM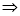
 ∥
∥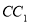 ,
,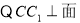 DCB
DCB  (这个证明很关键),然后根据公式
(这个证明很关键),然后根据公式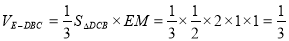 .
.
试题解析:
(1)在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点.
∴△DD1E为等腰直角三角形,∠D1ED=45°.同理∠C1EC=45°.
∴ ,即DE⊥EC.
,即DE⊥EC.
在长方体ABCD- 中,BC⊥平面
中,BC⊥平面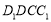 ,又DE
,又DE 平面
平面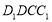 ,
,
∴BC⊥DE.又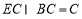 ,
,
∴DE⊥平面EBC.又
 ∴平面DEB⊥平面EBC.
∴平面DEB⊥平面EBC.
(2)取CD中点M,连接EM,
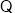 E为D1C1的中点,
E为D1C1的中点,
 ∥
∥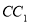 ,且
,且 ,
,
 又
又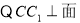 DCB
DCB

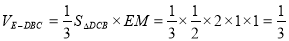 .
.
考点:线面垂直,三棱锥的体积.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016届福建省晋江市高一下学期期末考试数学试卷(解析版) 题型:选择题
若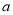 ,
,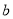 是异面直线,直线
是异面直线,直线 ∥
∥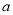 ,则
,则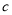 与
与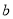 的位置关系是( )
的位置关系是( )
A.相交 B.异面 C.异面或相交 D.平行
查看答案和解析>>
科目:高中数学 来源:2016届福建省厦门市高一3月阶段测试数学试卷(解析版) 题型:填空题
如果一个水平放置的图形的斜二测直观图是一个底面为 ,腰和上底均为
,腰和上底均为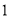 的等腰梯形,那么原平面图形的面积是_______-
的等腰梯形,那么原平面图形的面积是_______-
查看答案和解析>>
科目:高中数学 来源:2016届福建省厦门市高一3月阶段测试数学试卷(解析版) 题型:选择题
如图,用一平面去截球所得截面的面积为 ,已知球心到该截面的距离为1 ,则该球的体积是( )
,已知球心到该截面的距离为1 ,则该球的体积是( )

A.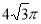


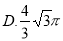
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com