
己知椭圆C: (a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,过F点的直线
(a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,过F点的直线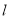 与椭圆C交于不同两点
与椭圆C交于不同两点 .
.
(1)求椭圆C的方程;
(2)设直线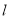 斜率为1,求线段
斜率为1,求线段 的长;
的长;
(3)设线段 的垂直平分线交
的垂直平分线交 轴于点P(0,y0),求
轴于点P(0,y0),求 的取值范围.
的取值范围.
(1)椭圆C的方程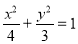 ;(2)线段
;(2)线段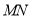 的长为
的长为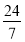 ;(3)
;(3)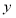 的取值范围是
的取值范围是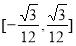 .
.
【解析】
试题分析:(1)根据椭圆的右焦点为F(1,0),点A(2,0)在椭圆C上,代入即可求得椭圆C的方程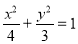 ;(2)先用点斜式
;(2)先用点斜式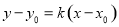 写出直线方程,再和椭圆方程联立,用弦长公式
写出直线方程,再和椭圆方程联立,用弦长公式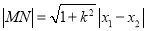 即可求出线段
即可求出线段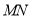 的长为
的长为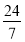 ;(3)当
;(3)当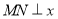 轴时,显然
轴时,显然 .当
.当 与
与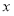 轴不垂直时,可设直线
轴不垂直时,可设直线 的方程为
的方程为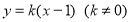 ,把直线方程与椭圆方程联立,设直线与椭圆的两个交点为
,把直线方程与椭圆方程联立,设直线与椭圆的两个交点为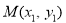 ,
, ,表示出
,表示出 ,联立即可求出
,联立即可求出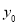 的取值范围.
的取值范围.
试题解析:(1)由题意: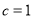 ,
,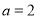 ,
,
 ,
,
所求椭圆方程为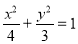 . 3分
. 3分
(2)由题意,直线l的方程为: .
.
由 得
得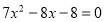 ,
,
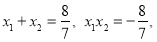
所以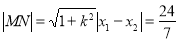 . 7分
. 7分
(3)当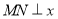 轴时,显然
轴时,显然 .
.
当 与x轴不垂直时,可设直线
与x轴不垂直时,可设直线 的方程为
的方程为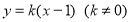 .
.
由 消去y整理得
消去y整理得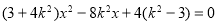 .
.
设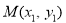 ,
, ,线段MN的中点为
,线段MN的中点为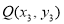 ,
,
则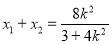 .
.
所以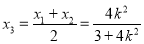 ,
,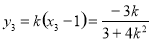
线段MN的垂直平分线方程为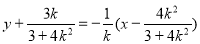
在上述方程中令x=0,得 .
.
当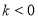 时,
时,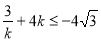 ;当
;当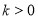 时,
时,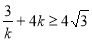 .
.
所以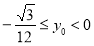 ,或
,或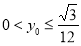 .
.
综上,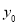 的取值范围是
的取值范围是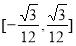 . 10分
. 10分
考点:直线与圆锥曲线的关系、函数与方程思想.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015届北京海淀区高二上学期期末考试理科数学试卷(解析版) 题型:选择题
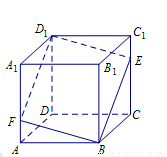
如图所示,在正方体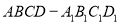 中,点
中,点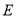 是棱
是棱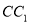 上的一个动点,平面
上的一个动点,平面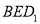 交棱
交棱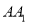 于点
于点 .则下列命题中假命题是( )
.则下列命题中假命题是( )
(A)存在点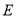 ,使得
,使得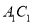 //平面
//平面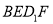
(B)存在点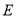 ,使得
,使得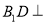 平面
平面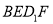
(C)对于任意的点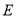 ,平面
,平面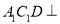 平面
平面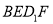
(D)对于任意的点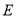 ,四棱锥
,四棱锥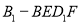 的体积均不变
的体积均不变
查看答案和解析>>
科目:高中数学 来源:2015届北京市西城区高二第一学期期末文科数学试卷(解析版) 题型:选择题
关于直线 以及平面
以及平面 ,下列命题中正确的是 ( )
,下列命题中正确的是 ( )
A. 若 ,则
,则 B. 若
B. 若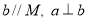 ,则
,则
C. 若 ,则
,则 D. 若
D. 若 ,则
,则
查看答案和解析>>
科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试理数学试卷(解析版) 题型:填空题
已知双曲线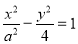 的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等于 .
的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等于 .
查看答案和解析>>
科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试理数学试卷(解析版) 题型:选择题
平面 平面
平面 的一个充分条件是
的一个充分条件是
A. 存在一条直线 ,
, 且
且
B. 存在一个平面 ,
, ∥
∥ 且
且 ∥
∥
C. 存在一个平面 ,
, ⊥
⊥ 且
且 ⊥
⊥
D. 存在一条直线 ,
, 且
且 ∥
∥
查看答案和解析>>
科目:高中数学 来源:2015届北京东城区高二第一学期期末考试文科数学试卷(解析版) 题型:选择题
抛物线 的准线与双曲线
的准线与双曲线  交于
交于 两点,点
两点,点 为抛物线的焦点,若△
为抛物线的焦点,若△ 为直角三角形,则双曲线的离心率为( )
为直角三角形,则双曲线的离心率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com