
| 证明:证法一:依题设得椭圆的半焦距c=1,右焦点为F(1,0),右准线方程为x=2,点E的坐标为(2,0),EF的中点为N( 若AB垂直于x轴,则A(1,y1),B(1,-y1),C(2,-y1), ∴AC中点为N( 若AB不垂直于x轴,由直线AB过点F,且由BC∥x轴知点B不在x轴上,故直线AB的方程为y=k(x-1),k≠0. 记A(x1,y1)和B(x2,y2),则(2,y2)且x1,x2满足二次方程 即(1+2k2)x2-4k2x+2(k2-1)=0 ∴ 又x12=2-2y12<2,得x1-
∴k1-k2=2k· ∵(x1-1)-(x2-1)(2x1-3)=3(x1+x2)-2x1x2-4 = ∴k1-k2=0,即k1=k2. 故A、C、N三点共线. 所以,直线AC经过线段EF的中点N. 证法二:如图,记直线AC与x轴的交点为点N,过点A作AD⊥l, 点D是垂足,因为点F是椭圆的右焦点,直线l是右准线, BC∥x轴,即BC⊥l,根据椭圆几何性质,得
∵AD∥FE∥BC, ∴ 即 ∴N为EF的中点,即直线AC经过线段EF的中点N. |


科目:高中数学 来源: 题型:解答题
 +y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.
+y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.查看答案和解析>>
科目:高中数学 来源: 题型:
(Ⅰ)求过点O、F,并且与椭圆的左准线l相切的圆的方程;
(Ⅱ)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
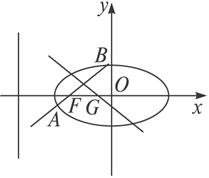
(1)求过点O、F,并且与椭圆的左准线l相切的圆的方程;
(2)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省莆田市仙游一中、六中高二(上)期末数学试卷(理科)(解析版) 题型:解答题
 +y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.
+y2=1的左、右焦点为F1、F2,上顶点为A,直线AF1交椭圆于B.如图所示沿x轴折起,使得平面AF1F2⊥平面BF1F2.点O为坐标原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com