
已知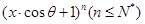 的展开式中,所有项的二项式系数之和为32,且展开式中含
的展开式中,所有项的二项式系数之和为32,且展开式中含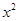 的系数与
的系数与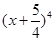 的展开式中
的展开式中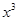 的系数相等,则锐角
的系数相等,则锐角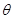 的值是
的值是
A. | B. | C. | D.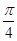 |
D
解析考点:二项式定理的应用;排列、组合的实际应用.
分析:由题意,(x?cosθ+1)n的展开式中二项式系数之和为32,即2n=32,可得n=5;由二项式定理求得(x?cosθ+1)n展开式中x2项的系数与(x+  )4的展开式中x3的系数,令两者相等根据题意,可得10cos2θ=5,解可得cos2θ=
)4的展开式中x3的系数,令两者相等根据题意,可得10cos2θ=5,解可得cos2θ= 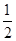 ,又由θ为锐角,可得cosθ的值,进而可得答案.
,又由θ为锐角,可得cosθ的值,进而可得答案.
解:由(x?cosθ+1)n(n≤N*)的展开式中二项式系数之和为32,得2n=32,则n=5;
故(x?cosθ+1)n(n≤N*)展开式中x2的系数为C53cos2θ=10cos2θ,
(x+ )4的展开式中x3的系数为
)4的展开式中x3的系数为 ?
? =5,
=5,
根据题意,有10cos2θ=5,则cos2θ=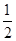 ,
,
又由θ为锐角,则cosθ=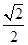 ,
,
即θ=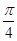 ;
;
故选D.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源:2013届江西省高二第二学期第一次月考理科数学试卷 题型:选择题
已知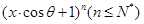 的展开式中,所有项的二项式系数之和为32,且展开式中含
的展开式中,所有项的二项式系数之和为32,且展开式中含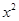 的系数与
的系数与 的展开式中
的展开式中 的系数相等,则锐角
的系数相等,则锐角 的值是
的值是
A. 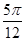 B.
B.
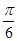 C.
C.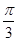 D.
D. 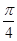
查看答案和解析>>
科目:高中数学 来源:2013届山东省济宁市高二3月月考理科数学试卷 题型:选择题
已知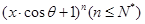 的展开式中,所有项的二项式系数之和为32,且展开式中含
的展开式中,所有项的二项式系数之和为32,且展开式中含 的系数与
的系数与 的展开式中
的展开式中 的系数相等,则锐角
的系数相等,则锐角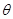 的值是( )
的值是( )
A.  B.
B.
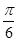 C.
C.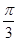 D.
D. 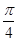
查看答案和解析>>
科目:高中数学 来源:2010-2011年江西省高二第二学期期中考试理科数学 题型:选择题
已知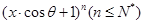 的展开式中,所有项的二项式系数之和为32,且展开式中含
的展开式中,所有项的二项式系数之和为32,且展开式中含 的系数与
的系数与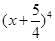 的展开式中
的展开式中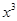 的系数相等,则锐角
的系数相等,则锐角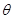 的值是
的值是
A.  B.
B.
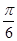 C.
C. D.
D. 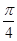
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广西柳州一中高三(上)第一次全市统测前模拟数学试卷(文科)(解析版) 题型:填空题
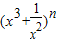 的展开式中,所有二项式系数的和为32,其展开式中的常数项为 (用数字答).
的展开式中,所有二项式系数的和为32,其展开式中的常数项为 (用数字答).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com