
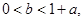 若关于
若关于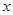 的不等式
的不等式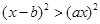 的解集中的整数恰有3个,则( )
的解集中的整数恰有3个,则( )A.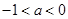 | B.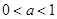 | C.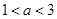 | D.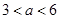 |
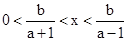
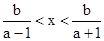 又由0<b<1+a得0<
又由0<b<1+a得0<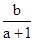 <1,
<1,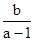 <-2,0<
<-2,0<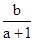 <1,这三个整数解必为-2,-1,0,2(a-1)<b≤3 (a-1),,注意到a>1,并结合已知条件0<b<1+a.,故要满足题设条件,只需要2(a-1)<1+a<3(a-1) 即可,则,b>2a-2,b<3a-3,又0<b<1+a,故 1+a>2a-2,3a-3>0解得1<a<3,综上1<a<3.故选C.
<1,这三个整数解必为-2,-1,0,2(a-1)<b≤3 (a-1),,注意到a>1,并结合已知条件0<b<1+a.,故要满足题设条件,只需要2(a-1)<1+a<3(a-1) 即可,则,b>2a-2,b<3a-3,又0<b<1+a,故 1+a>2a-2,3a-3>0解得1<a<3,综上1<a<3.故选C.

科目:高中数学 来源:不详 题型:单选题
 ,[0.5]=0,则使[x2-1]=3的x的取值范围是
,[0.5]=0,则使[x2-1]=3的x的取值范围是A.[2,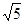 ) ) | B.(-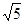 ,-2] ,-2] |
C.(-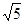 ,-2] ∪[2, ,-2] ∪[2,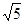 ) ) | D.[-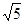 ,-2] ∪[2, ,-2] ∪[2,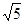 ] ] |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
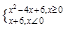 则不等式f(x)>f(1)的解集是( )
则不等式f(x)>f(1)的解集是( )| A.(-3,1)∪(3,+∞) | B.(-3,1)∪(2,+∞) |
| C.(-1,1)∪(3,+∞) | D.(-∞,-3)∪(1,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com