
【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表: 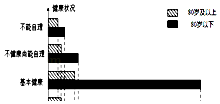
(1)若采取分层抽样的方法再从样本中的不能自理的老人中抽取16人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发 放生活补贴,标准如下:①80岁及以上长者每人每月发放生活补贴200元;②80岁以下 老人每人每月发放生活补贴120元;③不能自理的老人每人每月额外发放生活补贴100 元.试估计政府执行此计划的年度预算.
【答案】
(1)解:数据整理如下表:
健康状况 | 健康 | 基本健康 | 不健康尚能自理 | 不能自理 |
80岁及以上 | 20 | 45 | 20 | 15 |
80岁以下 | 200 | 225 | 50 | 25 |
从图表中知不能自理的80岁及以上长者占比为: ![]() =
= ![]() ,
,
故抽取16人中不能自理的80岁及以上长者人数为16× ![]() =6.80岁以下长者人数为10人
=6.80岁以下长者人数为10人
(2)解:在600人中80岁及以上长者在老人中占比为: ![]() =
= ![]() ,
,
用样本估计总体,80岁及以上长者共有 ![]() 万,
万,
80岁及以上长者占户籍人口的百分比为 ![]() 100%=2.75%
100%=2.75%
(3)解:用样本估计总体,设任一户籍老人每月享受的生活补助为X元,
P(X=0)= ![]() ,P(X=120)=
,P(X=120)= ![]() ×
× ![]() =
= ![]() ,P(X=200)=
,P(X=200)= ![]() =
= ![]() ,
,
P(X=220)= ![]() =
= ![]() ,P(X=300)=
,P(X=300)= ![]() =
= ![]() ,
,
则随机变量X的分布列为:
X | 0 | 120 | 220 | 300 | |
P |
|
|
|
|
|
EX=0× ![]() +120×
+120× ![]() +200×
+200× ![]() +220×
+220× ![]() +300×
+300× ![]() =28,
=28,
全市老人的总预算为28×12×66×104=2.2176×108元.
政府执行此计划的年度预算约为2.2176亿元
【解析】(1)数据整理如下表:
健康状况 | 健康 | 基本健康 | 不健康尚能自理 | 不能自理 |
80岁及以上 | 20 | 45 | 20 | 15 |
80岁以下 | 200 | 225 | 50 | 25 |
利用频率计算公式即可得出.(2)在600人中80岁及以上长者在老人中占比为: ![]() ,用样本估计总体,80岁及以上长者共有
,用样本估计总体,80岁及以上长者共有 ![]() 万,即可得出80岁及以上长者占户籍人口的百分比.(3)用样本估计总体,设任一户籍老人每月享受的生活补助为X元,P(X=0)=
万,即可得出80岁及以上长者占户籍人口的百分比.(3)用样本估计总体,设任一户籍老人每月享受的生活补助为X元,P(X=0)= ![]() ,P(X=120)=
,P(X=120)= ![]() ×
× ![]() ,P(X=200)=
,P(X=200)= ![]() ,P(X=220)=
,P(X=220)= ![]() ,P(X=300)=
,P(X=300)= ![]() ,及其数学期望.
,及其数学期望.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() .
.
(Ⅰ)证明:数列![]() 为等差数列,并求数列
为等差数列,并求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若记![]() 为满足不等式
为满足不等式![]() 的正整数
的正整数![]() 的个数,设
的个数,设![]() ,求数列
,求数列![]() 的最大项与最小项的值.
的最大项与最小项的值.
【答案】(1)见解析;(2)最大项为![]() ,最小项为
,最小项为![]() .
.
【解析】试题分析:(Ⅰ)对![]() 两边取倒数,移项即可得出
两边取倒数,移项即可得出![]() ,故而数列
,故而数列![]() 为等差数列,利用等差数列的通项公式求出
为等差数列,利用等差数列的通项公式求出![]() ,从而可得出
,从而可得出![]() ;(Ⅱ)根据不等式
;(Ⅱ)根据不等式![]() ,,得
,,得![]() ,又
,又![]() ,从而
,从而![]() ,当
,当![]() 为奇数时,
为奇数时,![]() 单调递减,
单调递减,![]() ;当
;当![]() 为偶数时
为偶数时![]() 单调递增,
单调递增,![]() 综上
综上![]() 的最大项为
的最大项为![]() ,最小项为
,最小项为![]() .
.
试题解析:(Ⅰ)由于![]() ,
,![]() ,则
,则![]()
∴![]() ,则
,则![]() ,即
,即![]() 为常数
为常数
又![]() ,∴数列
,∴数列![]() 是以1为首项,
是以1为首项,![]() 为公比的等比数列
为公比的等比数列
从而![]() ,即
,即![]() .
.
(Ⅱ)由![]() 即
即![]() ,得
,得![]() ,
,
又![]() ,从而
,从而![]()
故
当![]() 为奇数时,
为奇数时, ,
,![]() 单调递减,
单调递减,![]() ;
;
当![]() 为偶数时,
为偶数时, ,
,![]() 单调递增,
单调递增,![]()
综上![]() 的最大项为
的最大项为![]() ,最小项为
,最小项为![]() .
.
【题型】解答题
【结束】
22
【题目】已知向量![]() ,
,![]()
![]() ,若函数
,若函数![]() 的最小正周期为
的最小正周期为![]() ,且在区间
,且在区间![]() 上单调递减.
上单调递减.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若关于![]() 的方程
的方程![]() 在
在![]() 有实数解,求
有实数解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为  (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为 ![]() (α为参数),曲线C1上点P的极角为
(α为参数),曲线C1上点P的极角为 ![]() ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱ABC﹣A1B1C1的底面为正三角形,E,F分别是A1C1 , B1C1上的点,且满足A1E=EC1 , B1F=3FC1 . 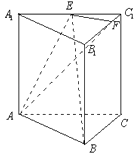
(1)求证:平面AEF⊥平面BB1C1C;
(2)设直三棱柱ABC﹣A1B1C1的棱长均相等,求二面角C1﹣AE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线C1 ![]() (t为参数),C2
(t为参数),C2 ![]() (θ为参数),
(θ为参数),
(Ⅰ)当α= ![]() 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
(Ⅱ)过坐标原点O做C1的垂线,垂足为A,P为OA中点,当α变化时,求P点的轨迹的参数方程,并指出它是什么曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() :方程
:方程 ![]() 有两个不等的正根;
有两个不等的正根; ![]() :方程
:方程 ![]() 表示焦点在
表示焦点在 ![]() 轴上的双曲线.
轴上的双曲线.
(1)若 ![]() 为真命题,求实数
为真命题,求实数 ![]() 的取值范围;
的取值范围;
(2)若“ ![]() 或
或 ![]() ”为真,“
”为真,“ ![]() 且
且 ![]() ”为假,求实数
”为假,求实数 ![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个 ![]() 列联表;
列联表;
(2)判断性别与休闲方式是否有关系.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com