
定义在R上的单调函数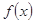 满足
满足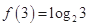 且对任意
且对任意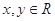 都有
都有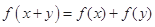 .
.
(1)求证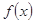 为奇函数;
为奇函数;
(2)若 对任意
对任意 恒成立,求实数
恒成立,求实数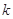 的取值范围.
的取值范围.
(1)利用赋值法证明抽象函数的奇偶性; (2) 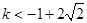
【解析】
试题分析:(1)f(x+y)=f(x)+f(y) ①,令x=y=0,代入①式得f(0+0)=f(0)+f(0),即f(0)=0
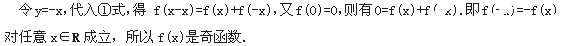
(2)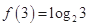 >0,即f(3)>f(0),又
>0,即f(3)>f(0),又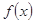 在R上是单调函数,所以
在R上是单调函数,所以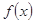 在R上是增函数
在R上是增函数
又由(1)f(x)是奇函数.f(k·3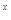 )<-f(3
)<-f(3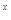 -9
-9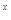 -2)=f(-3
-2)=f(-3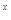 +9
+9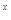 +2),
+2),
∴ k·3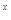 <-3
<-3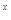 +9
+9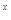 +2,3
+2,3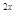 -(1+k)·3
-(1+k)·3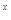 +2>0对任意x∈R成立.
+2>0对任意x∈R成立.
令t=3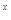 >0,问题等价于t
>0,问题等价于t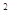 -(1+k)t+2>0
-(1+k)t+2>0
对任意t>0恒成立.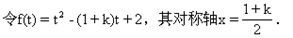
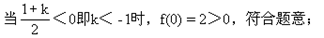

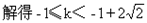
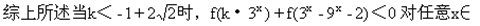 R恒成立.
R恒成立.
考点:本题考查了抽象函数的性质及运用
点评:在处理抽象函数的问题时,往往需要对某些变量进行适当的赋值,这是一般向特殊转化的必要手段。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2-x | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(-2-an) |
| 1 |
| 2 |
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
| 4 |
| 3 |
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| a2n |
| 12 |
| 35 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
| 1 |
| 2n |
| 4 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com