Question

设虚数z₁,z₂，满足.

(1)若z₁,z₂又是一个实系数一元二次方程的两根，求z₁, z₂。

(2)若z₁=1+mi(i为虚数单位，m∈R), ,复数w=z₂+3,求|w|的取值范围。

Answer 1

(1)  或   。

(2) .

解析:

(1)∵z₁, z₂是一个实系数一元二次方程的两个虚根，因此必共轭，

可设z₁=a+bi(a,b∈R且b≠0),则z₂=a－bi,

由 得(a+bi)²=a－bi

即： a²－b²+2abi=a－bi

根据复数相等，

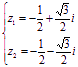∵b≠0 解得：   或   ，

∴  或   。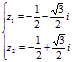

(2)由于 ，z₁=1+mi, w=z₂+3, 

∴w=(1+mi)²+3=4－m²+2mi.

∴ ,

由于且m≠0, 可解得0<m²≤1, 令m²=u, ,

在u∈(0,1)上，(u－2)²+12是减函数，∴.

复数这一章中去掉了三角形式,降低了难度，但在复数的基本概念、运算、复数与方程、复数与几何这些部分仍然有许多可考查的内容，并且还可以与其它的数学知识相结合。