【答案】
分析:将已知的等式左右两边平方,利用同角三角函数间的 基本关系求出2sinxcosx的值,再利用完全平方公式求出(sinx-cosx)
2的值,由x∈(0,π),得到sinx大于0,再由sinx+cosx的值小于0,得出x为钝角,可得出sinx-cosx大于0,cosx-sinx小于0,开方求出cosx-sinx的值,然后将所求式子利用二倍角的余弦函数公式化简后,把sinx+cosx及cosx-sinx的值代入即可求出值.
解答:解:把sinx+cosx=-

两边平方得:(sinx+cosx)
2=

,
∴sin
2x+2sinxcosx+cos
2x=1+2sinxcosx=

,即2sinxcosx=-

,
∴(sinx-cosx)
2=sin
2x-2sinxcosx+cos
2x=1-2sinxcosx=

,
∵x∈(0,π),
∴sinx>0,又sinx+cosx=-

<0,
∴x∈(
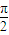
,π),
∴sinx-cosx=
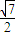
,即cosx-sinx=-

,
则cos2x=cos
2x-sin
2x=(cosx+sinx)(cosx-sinx)=-

×(-
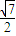
)=
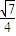
.
故选A
点评:此题考查了二倍角的余弦函数公式,同角三角函数间的基本关系,以及完全平方公式的运用,熟练掌握公式是解本题的关键.

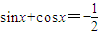 (其中x∈(0,π)),则cos2x的值为( )
(其中x∈(0,π)),则cos2x的值为( )
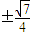
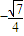
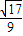
 两边平方得:(sinx+cosx)2=
两边平方得:(sinx+cosx)2= ,
, ,即2sinxcosx=-
,即2sinxcosx=- ,
, ,
, <0,
<0,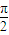 ,π),
,π),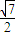 ,即cosx-sinx=-
,即cosx-sinx=- ,
, ×(-
×(-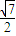 )=
)=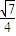 .
.
