
理 本小题满分12分)
|
(I)求三棱锥B – AB1D的体积;
(II)求证:BE⊥平面ADB1;
(Ⅲ)求二面角B—AB1—D的大小.
(I)![]() (Ⅲ)arcsin
(Ⅲ)arcsin![]()
(Ⅰ)∵AB=AC=a,∠BAC=90°,D为BC中点
B1B=C1C=A1A=2a,![]()
∴![]() ………………2分
………………2分
∵![]() …………4分
…………4分
解法一:(Ⅱ)由AB=AC,D是BC的中点,得AD⊥BC
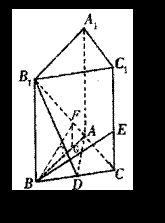 从而AD⊥平面B1BCC1 ,又BE
从而AD⊥平面B1BCC1 ,又BE![]() 平面B1BCC1,所在AD⊥BE …………6分
平面B1BCC1,所在AD⊥BE …………6分
由已知∠BAC=90°,AB=AC=a,得![]()
在Rt△BB1D中,
在Rt△CBE中,
于是∠BB1D=∠CBE,设EB∩DB1=G
∠BB1D+∠B1BG=∠CBE+∠B1BG=90°,则DB1⊥BE,又AD∩DB1=D
故BE⊥平面ADB1 ……………………8分
(Ⅲ)过点G作GF⊥AB1于F,连接BF
由(Ⅰ)及三垂线定理可知∠BFG是二面角B—AB1—D的平面角 …………10分
在Rt△ABB1中,由BF·AB1=BB1·AB,得![]()
在Rt△BDB1中,由BB1·BD=BG·DB1,得BG=![]()
所以在Rt△BFG中,![]()
故二面角B—AB—D的大小为arcsin![]() ………………12分
………………12分
解法二:
解法:(Ⅱ)如图,建立空间直角坐标系A-xyz …………2分
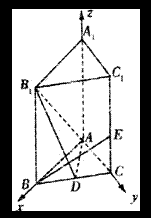 可知A(0,0,0),B(a,0,0),C(0,a,0),D(
可知A(0,0,0),B(a,0,0),C(0,a,0),D(![]() ),
),
B1(a,0,2a),E(0,a,![]() ) …………4分
) …………4分
可得 ![]()
![]() ………………6分
………………6分
于是得![]() ,
,
可知BE⊥AD,BE⊥DB1
又AD∩DB1=D,故BE⊥平面ADB1 …………8分
(Ⅲ)由(Ⅱ)知平面ADB1的法向量![]() ,平面ABB1的法向量
,平面ABB1的法向量![]()
于是 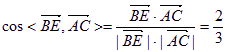 …………10分
…………10分
故二面角B—AB1—D的大小为arccos![]() ………………12分
………………12分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(2009山东卷理)(本小题满分12分)设函数f(x)=cos(2x+![]() )+sin
)+sin![]() x.
x.
(1) 求函数f(x)的最大值和最小正周期.
(2) 设A,B,C为![]() ABC的三个内角,若cosB=
ABC的三个内角,若cosB=![]() ,
,![]() ,且C为锐角,求sinA.
,且C为锐角,求sinA.
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009山东卷理)(本小题满分12分)
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q![]() 为0.25,在B处的命中率为q
为0.25,在B处的命中率为q![]() ,该同学选择先在A处投一球,以后都在B处投,用
,该同学选择先在A处投一球,以后都在B处投,用![]() 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
| 0 | 2 | 3 | 4 | 5 |
| 0.03 | P1 | P2 | P3 | P4 |
(1) 求q![]() 的值;
的值; ![]()
![]()
(2) 求随机变量![]() 的数学期望E
的数学期望E![]() ;
;
(3) 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
(江西卷理)(本小题满分12分)
 已知点
已知点![]() 为双曲线
为双曲线![]() (
(![]() 为正常数)上任一点,
为正常数)上任一点,![]() 为双曲线的右焦点,过
为双曲线的右焦点,过![]() 作右准线的垂线,垂足为
作右准线的垂线,垂足为![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于
轴于![]() .
. ![]()
![]()
(1) 求线段![]()
![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2) 设轨迹![]() 与
与![]() 轴交于
轴交于![]() 两点,在
两点,在![]() 上任取一点
上任取一点![]() ,直线
,直线![]() 分别交
分别交![]() 轴于
轴于![]() 两点.求证:以
两点.求证:以![]() 为直径的圆过两定点.
为直径的圆过两定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com