
 ,且1≤x、y、z、u≤10的所有四元有序整数组(x,y,z,u)的个数.
,且1≤x、y、z、u≤10的所有四元有序整数组(x,y,z,u)的个数.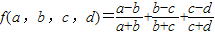 .记A:{(x,y,z,u)|1≤x,y,z,u≤10,f(x,y,z,u)>0},B:{(x,y,z,u)|1≤x,y,z,u≤10,f(x,y,z,u)<0},C:{(x,y,z,u)|1≤x,y,z,u≤10,f(x,y,z,u)=0},显然card(A)+card(B)+card(C)=104.下面证明:我们证明card(A)=card(B).接着计算card(C).而计算出满 足 x=z,y=u,x≠z的四元组共90个,进而可得答案.
.记A:{(x,y,z,u)|1≤x,y,z,u≤10,f(x,y,z,u)>0},B:{(x,y,z,u)|1≤x,y,z,u≤10,f(x,y,z,u)<0},C:{(x,y,z,u)|1≤x,y,z,u≤10,f(x,y,z,u)=0},显然card(A)+card(B)+card(C)=104.下面证明:我们证明card(A)=card(B).接着计算card(C).而计算出满 足 x=z,y=u,x≠z的四元组共90个,进而可得答案.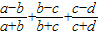 .
.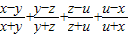 >0
>0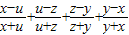 <0?f(x,y,z,u)<0?(x,u,z,y)∈B
<0?f(x,y,z,u)<0?(x,u,z,y)∈B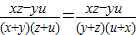 ?(z-x)(u-y)(xz-yu)=0
?(z-x)(u-y)(xz-yu)=0

科目:高中数学 来源:广东实验中学华南师附中广州市第六中学2007届高三级月考试卷(一)、数学(理工类)、(集合与逻辑、函数、导数? 题型:044
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
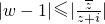 的点(x,y)表示的图形的面积.
的点(x,y)表示的图形的面积.查看答案和解析>>
科目:高中数学 来源:2006年四川省成都市高考数学一模试卷(理科)(解析版) 题型:解答题
 ,且对x,y∈(-1,1)时,有
,且对x,y∈(-1,1)时,有 .
. ,求数列{f(xn)}的通项公式;
,求数列{f(xn)}的通项公式; 的前n项和,问是否存在正整数m,使得对任意的n∈N*,有
的前n项和,问是否存在正整数m,使得对任意的n∈N*,有 成立?若存在,求出m的最小值;若不存在,则说明理由.
成立?若存在,求出m的最小值;若不存在,则说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com