
点A、B分别是椭圆![]() 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于![]() 轴上方,
轴上方,![]() .
.
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于![]() ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离![]() 的最小值.
的最小值.
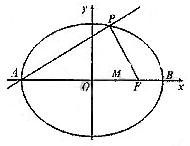
(1)由已知可得点A(-6,0),F(0,4)
设点P(![]() ,
,![]() ),则
),则![]() ={
={![]() +6,
+6, ![]() },
},![]() ={
={![]() -4,
-4, ![]() },由已知可得
},由已知可得
 则2
则2![]() +9
+9![]() -18=0,
-18=0, ![]() =
=![]() 或
或![]() =-6.
=-6.
由于![]() >0,只能
>0,只能![]() =
=![]() ,于是
,于是![]() =
=![]() . ∴点P的坐标是(
. ∴点P的坐标是(![]() ,
,![]() )
)
(2) 直线AP的方程是![]() -
-![]()
![]() +6=0. 设点M(
+6=0. 设点M(![]() ,0),则M到直线AP的距离是
,0),则M到直线AP的距离是![]() . 于是
. 于是![]() =
=![]() ,又-6≤
,又-6≤![]() ≤6,解得
≤6,解得![]() =2.
=2.
椭圆上的点(![]() ,
,![]() )到点M的距离
)到点M的距离![]() 有
有
![]() ,
,
由于-6≤![]() ≤6, ∴当
≤6, ∴当![]() =
=![]() 时,d取得最小值
时,d取得最小值![]()
设椭圆上动点坐标为(x,y),用该点的横坐标将距离d表示出来,利用求函数最值的方法求d的最小值. 点评:解决有关最值问题时,首先要恰当地引入变量(如点的坐标、角、斜率等),建立目标函数,然后利用函数的有关知识和方法求解.


科目:高中数学 来源: 题型:
 如图,点A、B分别是椭圆长轴的左、右端点,点F是椭圆的右焦点,其中A(-6,0),F(4,0),点P在椭圆上且位于x轴上方,
如图,点A、B分别是椭圆长轴的左、右端点,点F是椭圆的右焦点,其中A(-6,0),F(4,0),点P在椭圆上且位于x轴上方,| PA |
| PF |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省、大田中学高三3月联考文科数学试卷(解析版) 题型:解答题
已知椭圆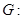
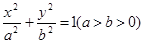 的离心率为
的离心率为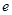 =
=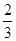 ,椭圆
,椭圆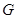 上的点
上的点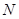 到两焦点的距离之和为12,点A、B分别是椭圆
到两焦点的距离之和为12,点A、B分别是椭圆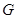 长轴的左、右端点,点F是椭圆的右焦点.点
长轴的左、右端点,点F是椭圆的右焦点.点 在椭圆上,且位于
在椭圆上,且位于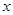 轴的上方,
轴的上方,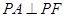 .
.
(I)
求椭圆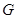 的方程;
的方程;
(II)求点 的坐标;
的坐标;
(III)
设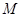 是椭圆长轴AB上的一点,
是椭圆长轴AB上的一点,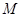 到直线AP的距离等于
到直线AP的距离等于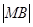 ,求椭圆上的点到点
,求椭圆上的点到点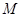 的距离
的距离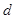 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年大纲版高三上学期单元测试(8)数学试卷 题型:解答题
(本小题满分12分)点A、B分别是椭圆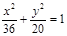 长轴的左、右端点,点F是
长轴的左、右端点,点F是
椭圆的右焦点,点P在椭圆上,且位于 轴上方,
轴上方,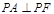 .
.
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于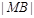 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2013届江苏省南通市高二第一学期期末考试数学 题型:解答题
.(本题满分16分)
点A、B分别是椭圆 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于 轴上方,
轴上方, .
.
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于 ,求点M的坐标;
,求点M的坐标;
(3)在(2)的条件下,求椭圆上的点到点M的距离 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com