
函数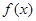 是定义在
是定义在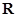 上的偶函数,且对任意的
上的偶函数,且对任意的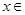
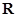 ,都有
,都有 .当
.当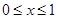 时,
时,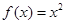 .若直线
.若直线 与函数
与函数 的图象有两个不同的公共点,则实数
的图象有两个不同的公共点,则实数 的值为( )
的值为( )
A.
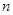
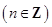 B.
B.
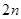
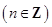
C.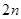 或
或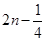
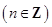 D.
D.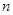 或
或
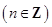
C
【解析】
试题分析:解:因为函数f(x)是定义在R上的偶函数,设x∈[-1,0],则-x∈[0,1],于是f(x)=(-x)2=x2.
设x∈[1,2],则(x-2)∈[-1,0].于是,f(x)=f(x-2)=(x-2)2.
①当a=0时,联立y="x," y=x2,解得x=0,y=0,或x=y=1,即当a=0时,即直线y=x+a与函数y=f(x)的图象有两个不同的公共点.
②当-2<a<0时,只有当直线y=x+a与函数f(x)=x2在区间[0,1)上相切,且与函数f(x)=(x-2)2在x∈[1,2)上仅有一个交点时才满足条件.由f′(x)=2x=1,解得x=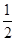 ∴y=(
∴y=(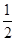 )2=
)2=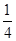 ,故其切点为(
,故其切点为(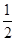 ,
,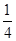 )
)
),∴a=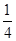 -
-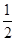 =-
=-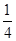 由y=x-
由y=x-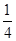 , y=(x-2)2(1≤x<2)解之得x=
, y=(x-2)2(1≤x<2)解之得x= 综上①②可知:直线y=x+a与函数y=f(x)在区间[0,2)上的图象有两个不同的公共点时的a的值为0或-
综上①②可知:直线y=x+a与函数y=f(x)在区间[0,2)上的图象有两个不同的公共点时的a的值为0或-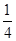 又函数f(x)是定义在R上的偶函数,且对任意的x∈R,都有f(x+2)=f(x),实数a的值为
又函数f(x)是定义在R上的偶函数,且对任意的x∈R,都有f(x+2)=f(x),实数a的值为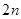 或
或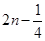 ,(n∈Z).故应选C.
,(n∈Z).故应选C.
考点:函数的奇偶性、周期性
点评:此题考查了函数的奇偶性、周期性及导数的应用,用到了数形结合的思想方法


科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:
已知![]() 是定义在
是定义在![]() 上的不恒为零的函数,且对于任意实数
上的不恒为零的函数,且对于任意实数![]() 都有
都有![]() , 则
, 则
(A)![]() 是奇函数,但不是偶函数 (B)
是奇函数,但不是偶函数 (B)![]() 是偶函数,但不是奇函数
是偶函数,但不是奇函数
(C)![]() 既是奇函数,又是偶函数 (D)
既是奇函数,又是偶函数 (D)![]() 既非奇函数,又非偶函
既非奇函数,又非偶函
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com