
 =(cosα,sinα),
=(cosα,sinα), =(cosβ,sinβ),0<β<α<π.(1)若|
=(cosβ,sinβ),0<β<α<π.(1)若| -
- |=
|= ,求证:
,求证: ⊥
⊥ ;(2)设c=(0,1),若
;(2)设c=(0,1),若 +
+ =c,求α,β的值.
=c,求α,β的值. 的坐标,求出
的坐标,求出 的坐标,由模等于
的坐标,由模等于 列式得到cosαcosβ+sinαsinβ=0,由此得到结论;
列式得到cosαcosβ+sinαsinβ=0,由此得到结论; +
+ ,由
,由 +
+ =(0,1)列式整理得到
=(0,1)列式整理得到 ,结合给出的角的范围即可求得α,β的值.
,结合给出的角的范围即可求得α,β的值. =(cosα,sinα),
=(cosα,sinα), =(cosβ,sinβ),
=(cosβ,sinβ), =(cosα-cosβ,sinα-sinβ),
=(cosα-cosβ,sinα-sinβ), =2-2(cosαcosβ+sinαsinβ)=2,
=2-2(cosαcosβ+sinαsinβ)=2, .即
.即 ;
;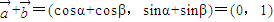
 ,①2+②2得:
,①2+②2得: .
. ,
, ,
, .
. .所以
.所以 .
. .
.

 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
在三角形ABC中,![]() =(cos
=(cos![]() ,sin
,sin![]() ),
), ![]() =(cos
=(cos![]() ,-sin
,-sin![]() 且
且![]() 的夹角为
的夹角为![]()
(1)求C;
(2)已知c=![]() ,三角形的面积S=
,三角形的面积S=![]() ,求a+b(a、b、c分别∠A、∠B、∠C所对的边)
,求a+b(a、b、c分别∠A、∠B、∠C所对的边)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
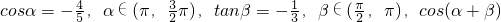 ,求cos(α+β).
,求cos(α+β).查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省绵阳市高考数学练习题(三)(解析版) 题型:解答题
 =(cosωx,sinωx),
=(cosωx,sinωx), =(cosωx,2
=(cosωx,2 cosωx-sinωx)(x∈R,ω>0)函数f(x)=|
cosωx-sinωx)(x∈R,ω>0)函数f(x)=|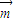 |+
|+ •
• 且最小正周期为π,
且最小正周期为π, ,求b的值.
,求b的值.查看答案和解析>>
科目:高中数学 来源:2010年高考真题分类精华版:三角函数(解析版) 题型:解答题
 ,求cos(α+β).
,求cos(α+β).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com