
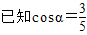 ,
,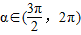 ,
,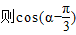 = .
= .  教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源:2009-2010学年山东省日照市实验高中高一(下)期末数学练习试卷9(必修3、4)(解析版) 题型:解答题
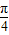 )sin(x-
)sin(x-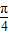 ).
).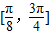 上的取值范围;
上的取值范围;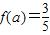 ,求m的值.
,求m的值.查看答案和解析>>
科目:高中数学 来源:2010-2011学年天津市东丽区百华实验中学高一(上)第二次月考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年浙江省金华一中高二(下)期中数学试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
科目:高中数学 来源:2011年山东省日照市实验高中高一(下)期末数学复习试卷13(必修3、4)(解析版) 题型:选择题
 cos6°-
cos6°-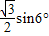 ,b=
,b=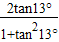 ,
,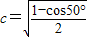 则有( )
则有( )查看答案和解析>>
科目:高中数学 来源:2009-2010学年山东省日照市实验高中高一(下)期末数学练习试卷9(必修3、4)(解析版) 题型:选择题
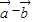 |=
|=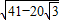 ,|
,|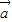 |=4,|
|=4,|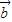 |=5,则
|=5,则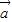 与
与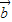 的数量积为( )
的数量积为( )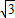
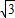
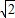
查看答案和解析>>
科目:高中数学 来源:2009-2010学年山东省日照市实验高中高一(下)期末数学练习试卷9(必修3、4)(解析版) 题型:选择题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年广东省珠海市斗门一中高二(上)期中数学试卷(文科)(解析版) 题型:填空题
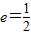 ,则椭圆的标准方程是 .
,则椭圆的标准方程是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com