
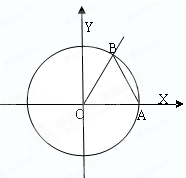
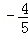 ,求tanα的值;
,求tanα的值;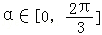 ,请写出弓形AB的面积S与α的函数关系式,并指出函数的值域.
,请写出弓形AB的面积S与α的函数关系式,并指出函数的值域.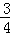
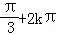 ,k∈Z}∪{β|β=
,k∈Z}∪{β|β=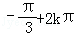 ,k∈Z}
,k∈Z}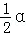 ﹣
﹣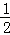 sinα,
sinα,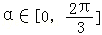 值域为:[0,
值域为:[0, ]
]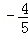 ,
,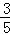 ),根据三角函数的定义得;
),根据三角函数的定义得;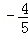 ,
,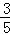 ),根据三角函数的定义得:tanα=
),根据三角函数的定义得:tanα= =﹣
=﹣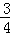 ;
; ,
,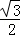 )或(
)或( ,
, )
)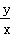 =
=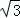 或
或 ,故∠AOB=
,故∠AOB=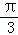 ,或
,或 ;
;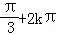 ,k∈Z}∪{β|β=
,k∈Z}∪{β|β=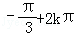 ,k∈Z};
,k∈Z};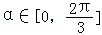 ,则S扇形=
,则S扇形= αr2=
αr2=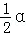 ,而S△AOB=
,而S△AOB= ×1×1×sinα=
×1×1×sinα= sinα,
sinα,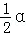 ﹣
﹣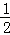 sinα,
sinα,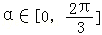 ,
,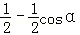 =
=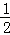 (1﹣cosα)>0,故S在区间
(1﹣cosα)>0,故S在区间 上单调递增,
上单调递增,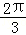 )=
)= ,
, ]
]

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源:不详 题型:解答题
 的
的 的函数
的函数 关系式;
关系式; 的值
的值查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com