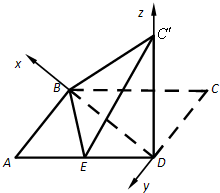
解:(Ⅰ)平行四边形ABCD中,AB=6,AD=10,BD=8,
沿直线BD将△BCD翻折成△BC'D
可知CD=6,BC’=BC=10,BD=8,
即BC'
2=C'D
2+BD
2,故CD⊥BD,C'D⊥BD.
∵平面BC'D⊥平面ABD,平面BC'D∩平面ABD=BD,C'D?平面BC'D,
∴C'D⊥平面ABD. …(4分)
如图,以D为原点,建立空间直角坐标系D-xyz.
则D(0,0,0),A(8,6,0),B(8,0,0),C'(0,0,6).
∵E是线段AD的中点,∴E(4,3,0),
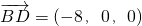
.
在平面BEC'中,
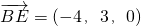
,
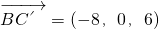
,
设平面BEC'法向量为

,
∴

,即
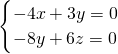
,
令x=3,得y=4,z=4,故
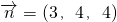
.
设直线BD与平面BEC'所成角为θ,则

.
∴直线BD与平面BEC'所成角的正弦值为
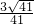
. …(9分)
(Ⅱ)由(Ⅰ)知平面BEC'的法向量为
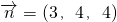
,而平面DBE的法向量为
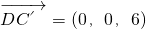
,
∴
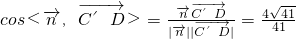
,
因为二面角D-BE-C'为锐角,
所以二面角D-BE-C'的余弦值为

. …(12分)
分析:(Ⅰ)先证明C'D⊥平面ABD,以D为原点,建立空间直角坐标系D-xyz.推出点D、A、B、C'的坐标,求出

,通过

求出平面BEC'法向量为

,利用

求直线BD与平面BEC'所成角的正弦值;
(Ⅱ)利用(Ⅰ)平面BEC'法向量为

,以及平面DBE的法向量
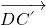
,通过

,求二面角D-BE-C'的余弦值.
点评:本题是中档题,考查直线与平面所成的角的求法,二面角的求法,正确建立空间直角坐标系求出平面的法向量是解题的关键,考查计算能力,空间想象能力.

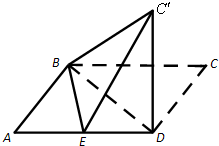 已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD.
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD. 解:(Ⅰ)平行四边形ABCD中,AB=6,AD=10,BD=8,
解:(Ⅰ)平行四边形ABCD中,AB=6,AD=10,BD=8,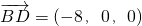 .
.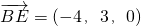 ,
,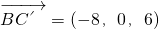 ,
, ,
, ,即
,即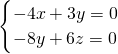 ,
,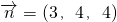 .
. .
.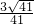 . …(9分)
. …(9分)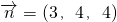 ,而平面DBE的法向量为
,而平面DBE的法向量为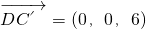 ,
,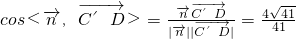 ,
, . …(12分)
. …(12分) ,通过
,通过 求出平面BEC'法向量为
求出平面BEC'法向量为 ,利用
,利用 求直线BD与平面BEC'所成角的正弦值;
求直线BD与平面BEC'所成角的正弦值; ,以及平面DBE的法向量
,以及平面DBE的法向量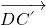 ,通过
,通过 ,求二面角D-BE-C'的余弦值.
,求二面角D-BE-C'的余弦值.


 ,试用
,试用 表示
表示 ;
; ;
; .
. ,试用
,试用 表示
表示 ;
; ;
; .
.