
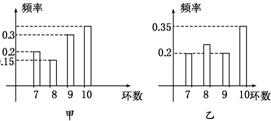
 甲、乙两射击运动员进行比赛,射击相同的次数,已知两运动员射击的环数稳定在7,8,9,10环,他们的成绩频率分布条形图如图:由乙击中8环及甲击中10环的概率与甲击中环数的平均值都正确的一组数据依次是
甲、乙两射击运动员进行比赛,射击相同的次数,已知两运动员射击的环数稳定在7,8,9,10环,他们的成绩频率分布条形图如图:由乙击中8环及甲击中10环的概率与甲击中环数的平均值都正确的一组数据依次是 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
 以下茎叶图记录了甲、乙两名射击运动员进行射击训练的成绩(环数),射击次数为4次.
以下茎叶图记录了甲、乙两名射击运动员进行射击训练的成绩(环数),射击次数为4次.| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:云南省昆明市2012届高中新课程高三摸底调研测试数学理科试题 题型:044
以下茎叶图记录了甲、乙两名射击运动员进行射击训练的成绩(环数),射击次数为4次.
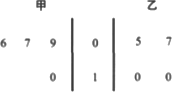
(Ⅰ)试比较甲、乙两名运动员射击水平的稳定性;
(Ⅱ)每次都从甲、乙两组数据中随机各选取一个进行比对分析,共选取了3次(有放回选取).设选取的两个数据中甲的数据大于乙的数据的次数为ξ,求ξ的分布列及期望.
(注:方差![]() ,其中
,其中![]() 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 以下茎叶图记录了甲、乙两名射击运动员进行射击训练的成绩(环数),射击次数为4次.
以下茎叶图记录了甲、乙两名射击运动员进行射击训练的成绩(环数),射击次数为4次.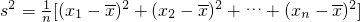 ,其中
,其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com