
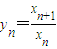 ,
,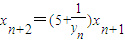 .n∈N*.
.n∈N*.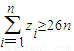 ;
;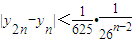 .
.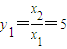 ,再根据yn的表达式和xn+2关于xn+1表达式,分别取n=1、2、3即可求出;
,再根据yn的表达式和xn+2关于xn+1表达式,分别取n=1、2、3即可求出;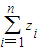 ,命题得证;
,命题得证;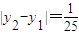
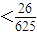 ,再通过yn+1关于yn的表达式,证出
,再通过yn+1关于yn的表达式,证出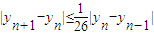 ,利用数列的递推特性进一步证出|yn+1-yn|≤
,利用数列的递推特性进一步证出|yn+1-yn|≤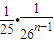 ,最后用绝对值不等式的性质将|y2n-yn|分解为不小于它本身的和:|yn+1-yn|+…+|y2n-1-y2n-2|+|y2n-y2n-1|的形式,得出等比数列求和表达式,再将所得结果适当放大,使命题得证.
,最后用绝对值不等式的性质将|y2n-yn|分解为不小于它本身的和:|yn+1-yn|+…+|y2n-1-y2n-2|+|y2n-y2n-1|的形式,得出等比数列求和表达式,再将所得结果适当放大,使命题得证.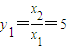 ,------------------------------------------------------------------------------2分
,------------------------------------------------------------------------------2分 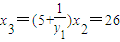 ,
,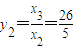 ,--------------------------------------------------------------------------3分
,--------------------------------------------------------------------------3分 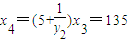 ,
, --------------------------------------------4分
--------------------------------------------4分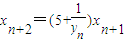 得
得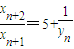 即
即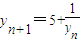 ⇒yn+1yn=5yn+1----------------------6分
⇒yn+1yn=5yn+1----------------------6分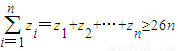 --------------------------------------------------------------------9分
--------------------------------------------------------------------9分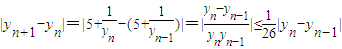
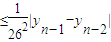
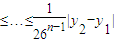 =
=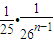 ----------------------------------------12分
----------------------------------------12分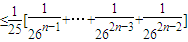 =
=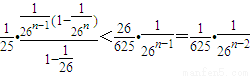
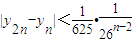 (n∈N*)----------------------------------------------14分
(n∈N*)----------------------------------------------14分

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
. | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com