
已知函数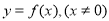 对于任意的
对于任意的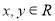 且
且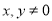 满足
满足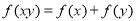 .
.
(1)求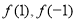 的值;
的值;
(2)判断函数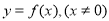 的奇偶性;
的奇偶性;
(3)若函数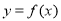 在
在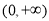 上是增函数,解不等式
上是增函数,解不等式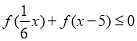 .
.
(1)0,0;(2)详见解析;(3) .
.
【解析】
试题分析:(1)根据已知宜用特殊值法,可令 进而求解
进而求解 ,在知
,在知 的前提下,可令
的前提下,可令 进而求解
进而求解 ;(2)证明抽象函数的奇偶性,关键在于构造
;(2)证明抽象函数的奇偶性,关键在于构造 ,故可令
,故可令 ,从而得出
,从而得出 ,结合(1)中相关结论,即可证明;(3)由
,结合(1)中相关结论,即可证明;(3)由 的奇偶性,结合已知可得其
的奇偶性,结合已知可得其 上的单调性,再逆用条件
上的单调性,再逆用条件 将
将 化为
化为 ,再结合(1)、(2)中所得结论及函数的单调性进行求解.
,再结合(1)、(2)中所得结论及函数的单调性进行求解.
试题解析:(1)∵对于任意的 且
且 满足
满足 ,
,
∴令 ,得到:
,得到: , ∴
, ∴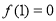 ,
,
令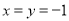 ,得到:
,得到: , ∴
, ∴ ;
;
(2)证明:由题意可知,函数 的定义域为
的定义域为 ,关于原点对称,
,关于原点对称,
令 ,得
,得 ,
,
∵ ,∴
,∴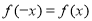 ,
,
∴ 为偶函数;
为偶函数;
(3)【解析】
由已知及 知不等式
知不等式 可化为
可化为 ,
,
又由函数 是定义在非零实数集上的偶函数且在
是定义在非零实数集上的偶函数且在 上是增函数,
上是增函数,
∴ ,即:
,即: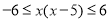 且
且 ,
,
解得: 或
或 且
且
故不等式的解集为: .
.
考点:1、抽象函数求值;2、抽象函数奇偶性判断;3、抽象不等式的求解;4、转化思想.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com