
甲乙两人连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图:
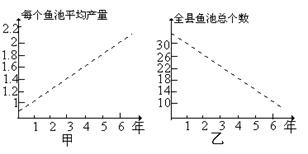
甲调查表明:每个鱼池平均产量从第1年1万只鳗鱼上升到第6年2万只。
乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个。
请你根据提供的信息说明:
(Ⅰ)第2年全县鱼池的个数及全县出产的鳗鱼总数。
(Ⅱ)到第6年这个县的鳗鱼养殖业的规模(即总产量)比第1年扩大了还是缩小了?说明理由。
(Ⅲ)哪一年的规模(即总产量)最大?说明理由。
(Ⅰ)第2年鱼池有26个,全县出产的鳗鱼总数为31.2万只.
(Ⅱ)第6年这个县的鳗鱼养殖业规划比第1年缩小了
(Ⅲ)当第2年时,鳗鱼养殖业的规模最大,最大产量为31.2万只.
由题意可知,图甲图象经过(1,1)和(6,2)两点,
从而求得其解析式为y甲=0.2x+0.8-----------------------(2分)
图乙图象经过(1,30)和(6,10)两点,
从而求得其解析式为y乙=-4x+34.------------------------- (4分)
(Ⅰ)当x=2时,y甲=0.2×2+0.8 =1.2,y乙= -4×2+34=26,
y甲·y乙=1.2×26=31.2.
所以第2年鱼池有26个,全县出产的鳗鱼总数为31.2万只.------------ ---(6分)
(Ⅱ)第1年出产鱼1×30=30(万只), 第6年出产鱼2×10=20(万只),可见,第6年这个县的鳗鱼养殖业规划比第1年缩小了----------------------------------(8分)
(Ⅲ)设当第m年时的规模总出产量为n,
那么n=y甲·y乙=(0.2m+0.8) (-4m+34)= -0. 8m2+3.6m+27.2
=-0.8(m2-4.5m-34)=-0.8(m-2.25)2+31.25---------------------------(11分)
因此, .当m=2时,n最大值=31.2.
即当第2年时,鳗鱼养殖业的规模最大,最大产量为31.2万只. --------------(14分)


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
 甲、乙两人连续6年对某农村养鸡业的规模进行调查,提供出以下两个不同的信息图及表.甲调查表明:每个养鸡场出产的鸡从第1年1万只上升到第6年2万只.(如表)
甲、乙两人连续6年对某农村养鸡业的规模进行调查,提供出以下两个不同的信息图及表.甲调查表明:每个养鸡场出产的鸡从第1年1万只上升到第6年2万只.(如表)| 年 | 1 | 2 | 3 | 4 | 5 | 6 |
| 鸡场养鸡平均只数 | 1.0万 | 1.2万 | 1.4万 | 1.6万 | 1.8万 | 2.0万 |
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高二版(必修5) 2009-2010学年 第2期 总第158期 北师大课标版(必修5) 题型:044
甲、乙两人连续
6年对某农村养鸡场的规模进行调查,提供两个不同信息如下图所示.
甲调查表明:从第
1年起每个养鸡场养殖1万只鸡上升到第6年平均每个养鸡场养殖2万只鸡.乙调查表明:由第
1年30个养鸡场减少到第6年10个养鸡场.请你根据提供的信息说明:(1)第2年养鸡场的个数及全县养殖鸡的总只数;
(2)到第6年,这个县的养鸡产业比第1年扩大了还是缩小了?请说明理由;
(3)哪一年的规模最大?请说明理由.
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高二版(A必修5) 2009-2010学年 第5期 总第161期 人教课标版(A必修5) 题型:044
甲、乙两人连续6年对某农村养鸡场的规模进行调查,提供两个不同信息(如下图所示).
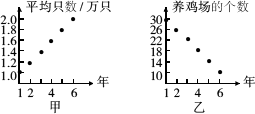
甲调查表明:从第1年起每个养鸡场养殖1万只鸡上升到第6年平均每个养鸡场养殖2万只鸡.
乙调查表明:由第1年30个养鸡场减少到第6年10个养鸡场.请你根据提供的信息说明:
(1)第2年养鸡场的个数及全县养殖鸡的总只数;
(2)到第6年,这个县的养鸡产业比第1年扩大了还是缩小了?请说明理由;
(3)哪一年的规模最大?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2002-2003学年北京市北大附中高三(上)期中数学试卷(解析版) 题型:解答题
| 年 | 1 | 2 | 3 | 4 | 5 | 6 |
| 鸡场养鸡平均只数 | 1.0万 | 1.2万 | 1.4万 | 1.6万 | 1.8万 | 2.0万 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com