Question

已知一个圆的摆线过一定点（1，0）,请写出该摆线的参数方程.

Answer 1

解析:根据圆的摆线的参数方程的表达式 (φ为参数),可知只需求出其中的r，也就是说，摆线的参数方程由圆的半径唯一确定，因此只需把点(1，0)代入参数方程求出r值再代入参数方程的表达式.

解:令r(1-cosφ)=0,可得cosφ=1.?

所以φ=2kπ(k∈Z)代入可得x=r(2kπ-sin2kπ)=1.?

所以r=.?

又根据实际情况可知r是圆的半径，故r＞0.?

所以应有k＞0且k∈Z，即k∈N^*.?

所以所求摆线的参数方程是

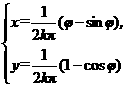(φ为参数)(其中k∈N^*).

点评:本题易错点是误把点(1，0)中的1或0当成φ的值，代入参数方程中求出x和y的值，再计算r的值；或者在求出cosφ=1后，直接得出φ=0，从而导致答案不全面.