Question

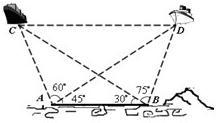
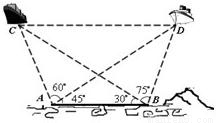
已知海岸边A，B两海事监测站相距60nmile，为了测量海平面上两艘油轮C，D间距离，在A，B两处分别测得∠CBD=75°，∠ABC=30°，∠DAB=45°，∠CAD=60°（A，B，C，D在同一个水平面内）．请计算出C，D两艘轮船间距离．

Answer 1

分析：在△ABD中先利用正弦定理求得AD，在△ABC中求得AC，然后在△ACD中，应用余弦定理求得CD．

解答：解：在△ABD中，由正弦定理得：

AD

sin∠ABD

=

AB

sin∠ADB

，
∴AD=

60sin(30°+75°)

sin[180°-(45°+30°+75°)]

=

60sin75°

sin30°

=

60× 6 + 2 4

1 2

=30(

6

+

2

)
同理，在△ABC中，由正弦定理得：

AC

sin∠ABC

=

AB

sin∠ACB

AC=

60sin30°

sin[180°-(45°+30°+60°)]

=

60× 1 2

sin45°

=

30

2 2

=30

2

在△ACD中，应用余弦定理计算出CD两点间的距离：
CD=

AC2+AD2-2AC•AD•cos60°

=

900×2+900( 6 + 2 )2-2×900 2 ( 6 + 2 )× 1 2

=

900×8+3600 3 +1800-1800 3 -1800

=

7200+1800 3

=30

8+2 3

∴C，D两艘轮船相距30

8+2 3

nmile．

点评：本题主要考查了解三角形的实际应用，正弦定理和余弦定理的综合运用．考查了三角函数基础知识的综合把握．