
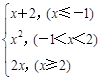 .
.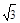 ;(3)见解析。
;(3)见解析。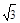 ,即t=
,即t=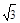 ;
;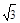 . ……8分
. ……8分

 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源:不详 题型:填空题
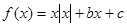 ,给出以下四个命题:①当c=0时,有
,给出以下四个命题:①当c=0时,有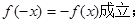 ②当b=0,c>0时,方程
②当b=0,c>0时,方程 ③函数
③函数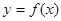 的图象关于点(0,c)对称 ④当x>0时;函数
的图象关于点(0,c)对称 ④当x>0时;函数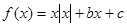 ,
, 。其中正确的命题的序号是_________。
。其中正确的命题的序号是_________。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 )=1,③对任意x,y
)=1,③对任意x,y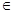 ( 0,+∞),
( 0,+∞),查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
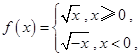 且
且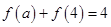 ,那么
,那么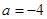 ;
;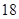 ,
,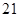 ,
,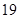 ,
,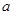 ,
,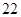 的平均数是
的平均数是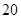 ,那么这组数据的方差是
,那么这组数据的方差是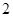 ;
; 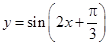 的图象,只要将
的图象,只要将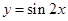 的图象向左平移
的图象向左平移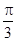 单位;
单位;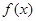 在
在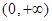 为增函数,且
为增函数,且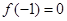 ,则不等式
,则不等式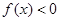 的解集为
的解集为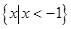 .
. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com