
 给出函数f(x)的下列五个结论:①最小值为
给出函数f(x)的下列五个结论:①最小值为 ; ②一个单增区间是(
; ②一个单增区间是( ,
, );③其图象关于直线
);③其图象关于直线 (k∈Z)对称; ④最小正周期为2π; ⑤将其图象向左平移
(k∈Z)对称; ④最小正周期为2π; ⑤将其图象向左平移 后所得的函数是奇函数. 其中正确结论的个数是( )
后所得的函数是奇函数. 其中正确结论的个数是( )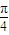 ,2kπ+
,2kπ+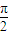 ],[2kπ+
],[2kπ+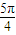 ,2kπ+2π](k∈Z),
,2kπ+2π](k∈Z),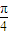 ],[2kπ+
],[2kπ+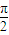 ,2kπ+
,2kπ+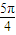 ](k∈Z),
](k∈Z),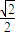 .
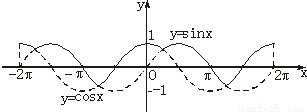
.
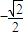 ;正确;
;正确;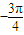 ,
,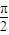 ),错误;
),错误;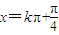 (k∈Z)对称;正确;
(k∈Z)对称;正确;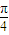 后所得的函数是奇函数.错误,是偶函数.
后所得的函数是奇函数.错误,是偶函数.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:013
已知函数f ( x ) =-x-x3,对于满足条件x1+x2 > 0,x2+x3 > 0,x3+x1 > 0的任意实数x1,x2,x3给出下列四个结论:
① f ( x1 )+ f ( x2 )+ f ( x3 )的值一定为正数;
② f ( x1 )+ f ( x2 )+ f ( x3 )的值一定为负数;
③ f ( x1 )+ f ( x2 )+ f ( x3 )的值一定为零;
④ f ( x1 )+ f ( x2 )+ f ( x3 )的值可能为正数,也可能为负数.
其中正确结论的个数是( ).
|
(A) 1 |
(B) 2 |
|
(C) 3 |
(D) 4 |
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
① f ( x1 )+ f ( x2 )+ f ( x3 )的值一定为正数;
② f ( x1 )+ f ( x2 )+ f ( x3 )的值一定为负数;
③ f ( x1 )+ f ( x2 )+ f ( x3 )的值一定为零;
④ f ( x1 )+ f ( x2 )+ f ( x3 )的值可能为正数,也可能为负数.
其中正确结论的个数是( ).
|
(A) 1 |
(B) 2 |
|
(C) 3 |
(D) 4 |
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
① f ( x1 )+ f ( x2 )+ f ( x3 )的值一定为正数;
② f ( x1 )+ f ( x2 )+ f ( x3 )的值一定为负数;
③ f ( x1 )+ f ( x2 )+ f ( x3 )的值一定为零;
④ f ( x1 )+ f ( x2 )+ f ( x3 )的值可能为正数,也可能为负数.
其中正确结论的个数是 ( )
(A) 1 (B) 2 (C) 3 (D) 4
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 给出函数f(x)的下列五个结论:①最小值为
给出函数f(x)的下列五个结论:①最小值为 ; ②一个单增区间是(
; ②一个单增区间是(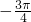 ,
, );③其图象关于直线
);③其图象关于直线 (k∈Z)对称; ④最小正周期为2π; ⑤将其图象向左平移
(k∈Z)对称; ④最小正周期为2π; ⑤将其图象向左平移 后所得的函数是奇函数. 其中正确结论的个数是
后所得的函数是奇函数. 其中正确结论的个数是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com