
| A. | 1:3 | B. | 1 | C. | 5:3 | D. | 3:5 |
分析 以O为原点,作单位向量$\overrightarrow{O{A}^{'}}$,$\overrightarrow{O{B}^{'}}$,$\overrightarrow{O{C}^{'}}$,让它们两两夹角为120°,在OA'上取A点,使$\overrightarrow{O{A}^{'}}$=$\overrightarrow{OA}$,在OB'上取B点,使$\overrightarrow{O{B}^{'}}=3\overrightarrow{OB}$,在OC'上取C点,使$\overrightarrow{O{C}^{'}}=5\overrightarrow{OC}$,由此能求出△OAB与△OAC的面积之比.
解答 解:∵O是△ABC中的一点,$\overrightarrow{OA}+3\overrightarrow{OB}+5\overrightarrow{OC}=\overrightarrow 0$,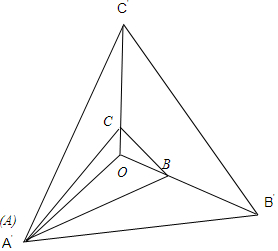
∴以O为原点,作单位向量$\overrightarrow{O{A}^{'}}$,$\overrightarrow{O{B}^{'}}$,$\overrightarrow{O{C}^{'}}$,让它们两两夹角为120°,
则$\overrightarrow{O{A}^{'}}+\overrightarrow{O{B}^{'}}+\overrightarrow{O{C}^{'}}$=$\overrightarrow{0}$,
在OA'上取A点,使$\overrightarrow{O{A}^{'}}$=$\overrightarrow{OA}$,
在OB'上取B点,使$\overrightarrow{O{B}^{'}}=3\overrightarrow{OB}$,
在OC'上取C点,使$\overrightarrow{O{C}^{'}}=5\overrightarrow{OC}$,
所以$\overrightarrow{OA}$+3$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow 0$,
因为S△ABC=$\frac{1}{2}absinC$,
所以△OAB与△OAC的面积之比为:
$\frac{{S}_{△OAB}}{{S}_{△OAC}}$=$\frac{\frac{1}{2}×|\overrightarrow{OA}|•|\overrightarrow{OB}|×sin120°}{\frac{1}{2}×|\overrightarrow{OA}|×|\overrightarrow{OC}|×sin120°}$=$\frac{|\overrightarrow{OB}|}{|\overrightarrow{OC}|}$=$\frac{\frac{1}{3}}{\frac{1}{5}}$=5:3.
故选:C.
点评 本题考查两个三角形面积之比的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
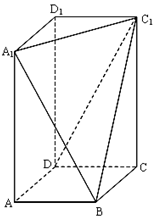 已知长方体ABCD-A1B1C1D1,其中AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的,且这个几何体的体积为$\frac{40}{3}$.
已知长方体ABCD-A1B1C1D1,其中AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的,且这个几何体的体积为$\frac{40}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0}⊆M | B. | M=∅ | C. | -1∈M | D. | 2∈M |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com